Risolvi, usando del software, graficamente e numericamente, la seguente disequazione. Prova, quindi, a risolverla "esattamente".

2·|3+5·x−2·x²| < 1−x

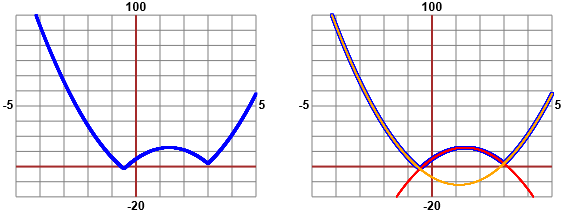
Se provo a tracciare il grafico di y = 2·|3+5·x−2·x²| - (1−x) ottengo la rappresentazione seguente, a sinistra.

Se distinguo i casi in cui l'argomento del valore assoluto è positivo o negativo ottengo le due curve (parabole) rappresentate a destra:
y = 2*(3+5*x-2*x*x)-(1-x) = -4*x²+11*x+5 (rossa)  e  y = 4*x²-9*x-7 (arancione).
Con uno zoom verifico se la curva tocca l'asse x a destra dell'origine: vedo che ciò non accade.

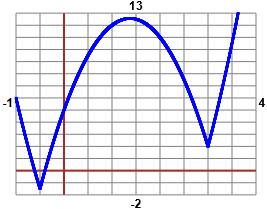
I grafici sono stati tracciati usando questo script.

Quindi vi sono due valori, A, di poco inferiore a -0.5, e B, di poco superiore a -0.5, per cui le soluzioni costituiscono l'intervallo (A, B). Sono soluzioni delle equazioni di secondo grado rappresentate dalle due parabole. Posso risolvere le due equazioni a mano. Facciamolo con lo script semplici equazioni:

Dunque l'intervallo soluzione, con gli estremi arrotondati, è (-0.611555498681226, -0.397180859844728).  Risolvendo a mano avremmo trovato le soluzioni "esatte", che possiamo comunque trovare con WolframAlpha introducendo -0.611555498681226 e poi -0.397180859844728:

1/8*(9 - sqrt(193))       1/8*(11 - sqrt(201))

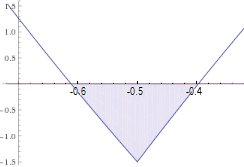
Con WolframAlpha potrei introdurre direttamente 2*abs(3+5*x-2*x^2)-(1-x) < 0 e ottenere sia le soluzioni che la rappresentazione grafica seguente:

Come avrei potuto utilizzare R:

source("http://macosa.dima.unige.it/r.R")
f = function(x) 2*abs(3+5*x-2*x^2)-(1-x)
graficoF( f, -10,10, 1)
   
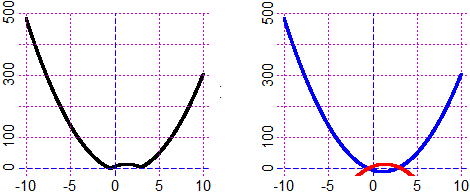# Ho ottenuto il grafico sopra a sinistra. Posso pensarlo originato da due parabole:
g = function(x) 2*(3+5*x-2*x^2)-(1-x); h = function(x) -2*(3+5*x-2*x^2)-(1-x)
# Potrei semplificare questi termini, ma (per ora) non mi serve farlo ...
grafico( h, -10,10, "blue"); grafico( g, -10,10, "red")   * o  "graph" invece di "grafico"
# Faccio degli zoom:
graficoF( f, -2,4, 1)         * o  "graphF" invece di "graficoF"
graficoF( f, -1,0, 1)
graficoF( f, -0.62,-0.39, 1)
   
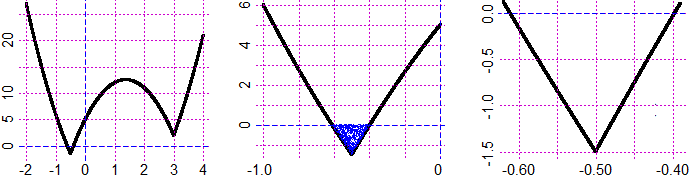# Capisco che la soluzione č A < x < B con A circa -0.6 e B circa -0.4.
# Risolvo le equazioni col software:
soluz(f,0, -0.5,-0.2)     # [1] -0.3971809   [o  "solution" invece di "soluz"]
soluz(f,0, -0.8,-0.5)     # [1] -0.6115555
# o, per avere pių cifre  (nota: la seconda non ha periodo 5):
piu( soluz(f,0, -0.5,-0.2) ); piu( soluz(f,0, -0.8,-0.5) )     # o  "more" invece di "piu"
#    -0.397180859844728   <  x  <  -0.611555498681226

Volendo le soluzioni esatte risolvo a mano le equazioni g(x)=0 e h(x)=0,
ossia:   -4*x^2+11*x+5=0  4*x^2-9*x-7=0
Ottengo:    (9-sqrt(193))/8 < x < (11-sqrt(201))/8
# I pallini blu nella figura sopra al centro, che rappresentano le soluzioni, sono
# stati ottenuti con R risolvendo la disequazione graficamente:
Z = function(x) 0; diseq(f,Z, -1,0, "blue")
# Se voglio una punteggiatura pių fitta:   for(i in 1:5) diseq(f,Z, -1,0, "blue")
#
# Volendo potevo ragionare sui due termini 2*abs(3+5*x-2*x^2) e 1-x
#
P = function(x) 2*abs(3+5*x-2*x^2); Q = function(x) 1-x
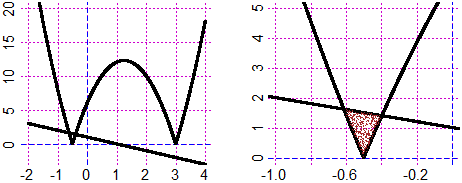
Piano(-2,4, -2,20); grafico ( Q, -2,4, 1); grafico ( P, -2,4, 1)   # o "Plane" invece di "Piano"
Piano(-1,0, 0,5); grafico ( P, -2,4, 1); grafico ( Q, -2,4, 1)
for(i in 1:5) diseq(P,Q, -1,0, "brown")
     
soluz2(P,Q, -0.8,-0.5); soluz2(P,Q, -0.5,-0.2)
#   -0.6115555             -0.3971809