Risolvi, usando del software, graficamente e numericamente, la seguente disequazione. Prova, quindi, a risolverla "esattamente", eventualmente usando altro software.

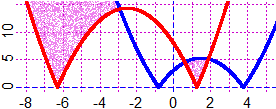
|x²−3·x−3| > |x²+5·x−8|

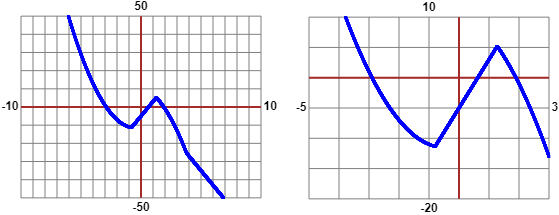
Se provo a tracciare il grafico di y = |x²−3·x−3| - |x²+5·x−8| ottengo le rappresentazioni seguenti:

Se distinguo i casi in cui l'argomento del valore assoluto è positivo o negativo ottengo le due curve (retta e parabola) rappresentate sotto:
y = (x*x-3*x-3)-(x*x+5*x-8) = -8*x+5 (rossa)  e  y = (x*x-3*x-3)+(x*x+5*x-8) = 2*x²+2*x-11 (arancione), e le loro simmetriche rispetto all'asse x (ottenute cambiando i segni).

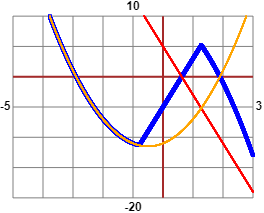
Quindi vi sono tre valori, A (circa -3), B (circa 0.6) e C (circa 1.9) tali che le soluzioni costituiscono gli intervalli (-∞, A) e (B, C). Posso risolvere le due equazioni  -8*x+5=0  e  2*x²+2*x-11=0  a mano. Facciamolo con lo script semplici equazioni:

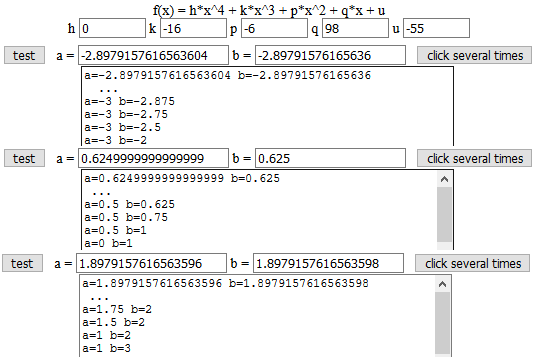
Dunque i valori arrotondati sono A = -2.89791576165636, B = 0.625, C = 1.89791576165636..  Risolvendo a mano avremmo trovato le soluzioni "esatte", che possiamo comunque trovare con WolframAlpha introducendo -2.89791576165636 e poi1.89791576165636:

1/2*(-1 - sqrt(23)       1/2*(sqrt(23) - 1)

Con WolframAlpha potrei introdurre direttamente solve abs(x^2-3*x-3) > abs(x^2+5*x-8) for x real per risolvere la disequazione (se non metto "real" posso ottenere delle uscite in forma "strana").

Posso osservare che |U| > |V| quando U² > V². Posso quindi anche studiare il segno di: (x^2-3*x-3)^2-(x^2+5*x-8)^2, ossia di -16*x^3-6*x^2+98*x-55. Per risolvere -16*x^3-6*x^2+98*x-55 = 0 posso usare questo script, ritrovando i valori trovati in precedenza:

Come avrei potuto utilizzare R:

# Studio, equivalentemente, dove è maggiore di 0 la f seguente:
# (invece di "grafico", "soluz", "piu" posso usare "graph", "solution", "more")
source("http://macosa.dima.unige.it/r.R")
f = function(x) abs(x^2-3*x-3)-abs(x^2+5*x-8)
graficoF (f, -10,10, 1)
graficoF (f, -4,3, 1)

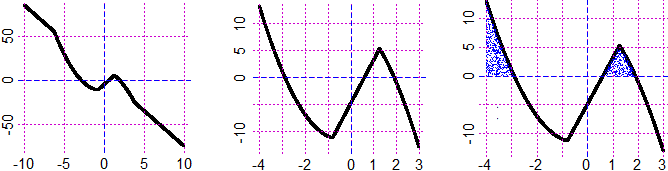# Il grafico a destro l'ho ottenuto aggiungendo:
Z = function(x) 0; diseq(Z,f, -4,3, "blue")
# Le soluzioni sono "circa" x < -3, 0.5 < x < 2. Trovo i valori con R:
soluz(f,0, -5,0)     # [1] -2.897916
soluz(f,0, 0,1)      # [1] 0.625
soluz(f,0, 1,3)      # [1] 1.897916
piu( soluz(f,0, -5,0) ); piu( soluz(f,0, 1,3) )
#     -2.89791576165636      1.89791576165636
#
# Ovvero posso studiare direttamente le due funzioni:
Plane(-8,5, 0,15)
graph(f1,-10,10, "blue"); graph(f2,-10,10, "red")
diseq(f2,f1, -9,6, "violet")
more(solution2(f1,f2, -4,-2))
# -2.89791576165636
more(solution2(f1,f2, 0,1))
# 0.625
more(solution2(f1,f2, 1,2))
# 1.89791576165636