Studia il segno del seguente termine in x. Usa del software per risolvere il problema graficamente e numericamente. Prova, quindi, a risolverlo "esattamente", eventualmente usando altro software.

x⁴ − 4·x² + 2
——————
x³ − 7

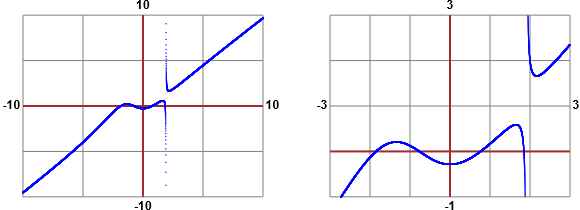
Il termine non è definito per x = ³√7 = 1.91293118277238...  Tracciamo il grafico di y = "termine":

A questo punto posso trovare facilmente dove si azzera il termine mediante lo script solve polinomial equation (con h=1, p=-4, u=2) partendo da a=-2, b=-1, da a=-1, b=0, da a=0, b=1, da a=1, b=1.99:

Trovo:   a=-1.8477590650225737, b=-1.8477590650225735;   a=-0.7653668647301797, b=-0.7653668647301796;   a=0.7653668647301795, b=0.7653668647301796;   a=1.8477590650225733, b=1.8477590650225735
Concludendo il termine è positivo  in (-1.8477590650225735, -0.7653668647301796),  in (0.7653668647301796, 1.8477590650225735),  in (7, ∞).

I grafici sono stati tracciati usando questo script.

Posso ottenere le forme esatte dei valori ottenuti mettendo in WolframAlpha i valori approssimati. Ottengo:

Potevo con WolframAlpha trovare direttamente le soluzioni introducendo (x^4-4*x^2+2)/(x^3-7) > 0

Come avrei potuto utilizzare R:

# Per R vedi qui
source("http://macosa.dima.unige.it/r.R")   # se non hai gią caricato il file
f = function(x) (x^4-4*x^2+2)/(x^3-7)
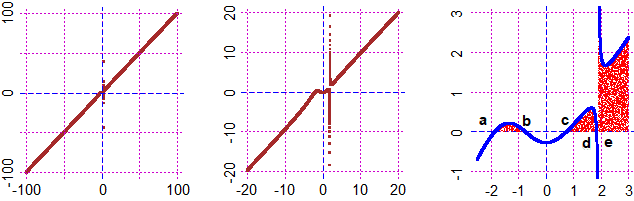
BF=2.5; HF=2.5; graphF(f, -100,100, "brown")
Plane(-20,20, -20,20); graph(f, -20,20,"brown") 
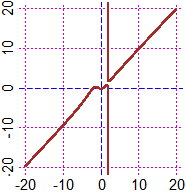
# Il grafico sottostante è stato tracciato pił sottile (con "graph2" - largo
# 2 pixel - al posto di "graph"), e ritracciato nell'intervallo in cui
# appariva punteggiato
Plane(-2.5,3, -1,3); graph(f, -2.5,3,"brown")
# Con le due righe seguenti evidenzio dove f(x) > 0
zero = function(x) 0
Diseq(zero,f, -2.5,3, "red"); graph(f, -2.5,3,"blue")
# Le etichette dei punti in cui la funzione cambia segno:
text(-2.3,0.3,"a",font=2,cex=0.9); text(-0.7,0.3,"b",font=2,cex=0.9)
text(0.7,0.3,"c",font=2,cex=0.9); text(1.5,-0.25,"d",font=2,cex=0.9)
text(2.3,-0.25,"e",font=2,cex=0.9)
a=solution(f,0, -2,-1.5); more(a)    #  -1.84775906502257
b=solution(f,0, 0,-1.5); more(b)     #  -0.76536686473018
c=solution(f,0, 0,1); more(c)        #  0.76536686473018
d=solution(f,0, 1.91,1); more(d)     #  1.84775906502257
e=rad3(7); more(e)                   #  1.91293118277239

Il termine è positivo in  (a, b), in  (c, d)  e in  (e, ∞).