1) F: x
(2x3 – 24x2 + 40x) / (x(10 – x))2) G: y
(y4 – 6πy3 + 9π2y2) / (y – 3π)43) H: x
(3x2 – 9x + 6) / (x2 – 5x + 6)
Devo calcolare ripetutamente, per diversi input, i valori delle seguenti funzioni. Vedi se è possibile esprimerle in modo da semplificare i calcoli.
1) F: x (2x3 – 24x2 + 40x) / (x(10 – x))
2) G: y (y4 – 6πy3 + 9π2y2) / (y – 3π)4
3) H: x (3x2 – 9x + 6) / (x2 – 5x + 6)
1) 2x3 – 24x2 + 40 x è fattorizzabile in 2x(x2 – 12x + 20), per cui, per x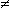
0, F(x) equivale a 2(x2 – 12x + 20)/(10 – x).
A questo punto, tenendo conto che 10 – x = –(x – 10) provo a dividere x2 – 12x + 20 per x–10. Ottengo: x–2 con resto 0. Quindi F(x) equivale a:
–2(x–2), restringendo il dominio a: x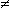0 AND x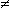10.
Del resto se avessi tracciato il grafico di F (col computer o a mano, tabulando qualche valore) avrei subito capito che, nel suo dominio, F equivale a x –2x+2.
Un metodo più pedestre (e dispendioso) sarebbe stato quello di usare le formulette per risolvere le equazioni di secondo grado per scomporre x2 – 12x + 20.
2) y4 – 6πy3 + 9π2y2 è fattorizzabile in y2(y2 – 6πy + 9π2). Posso osservare che se al posto di y metto 3π ottengo 0, concludere che questo termine è divisibile per y–3π, eseguire la divisione, ecc.. Ma posso anche osservare, ricordando lo sviluppo di (a+b)2, che y2–6πy+9π2 = (y–3π)2. In entrambi i modi ottengo che G(y) equivale a:
y2/(y–3π)2, o, meglio, a: (y/(y–3π))2
[che, se devo usare una calcolatrice, mi conviene trasformare in: (1+3π/(y–3π))2 (ho eseguito la divisione) e, infine, in: (1+1/(y/3/π–1))2,
in modo che, battuto (una sola volta) y, posso procedere con:
3 
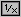
1 
1 
]
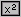3) Posso procedere con divisioni successive:
(3x2 – 9x + 6) / (x2 – 5x + 6) = 3 + (6x – 12) / (x2 – 5x + 6) (ho fatto la divisione);
(x2 – 5x + 6) / (6x – 12) = 1/6 x – 1/2 (ho fatto la divisione);
quindi: (3x2 – 9x + 6) / (x2 – 5x + 6) = 3 + 1 / (1/6 x – 1/2) =
Ovvero dalle divisioni successive potevo concludere che 6x-12, ovvero x-2, è un m.c.d. dei due polinomi, dividerli entrambi per x-2 ottenendo:
(3x2 – 9x + 6) / (x2 – 5x + 6) = (3x – 3) / (x – 3) che poi potevo trasformare (dividendo) in 3 + 6 / (x – 3).
Oppure potevo osservare che per x=2 entrambi i polinomi si annullano e da qui decidere di dividerli entrambi per x-2.
In ogni caso devo escludere x–2 = 0, ossia porre x 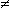2.
Potrei controllare gli esiti con WolframAlpha. Per es. nell'ultimo caso introdotto (3x^2–9x+6)/(x^2–5x+6) ottengo: 6/(x-3)+3 (for x≠2).
Per altri commenti: 
fuzioni polinomiali neGli Oggetti Matematici.