(a)  Trova m.c.d. e m.c.m. (con coefficiente direttivo 1) tra le seguenti coppie di polinomi (usa le tracce proposte).

x2−4  e  x2−5x+6 [osserva che x2−4 è scomponibile in ... e usa il teorema del resto in modo opportuno sull'altro polinomio]
x2−6x+5  e  x2−6x+8 [che relazione c'è tra i grafici di x → x2−6x+5 e di x → x2−6x+8? possono avere in comune intersezioni con l'asse x? possono essere entrambi divisibili per uno stesso polinomio di 1º grado?]
x3−2x2+x−2  e  x3−2x2+x+1   [utilizza l'algoritmo euclideo]

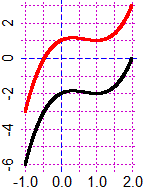
(b)  Stabilisci se le figure di equazione y = x3−2x2+x−2  e  y = x3−2x2+x+1  hanno in comune intersezioni con l'asse x. Verifica la cosa tracciando i loro grafici.

(a)  x2–4 = (x–2)(x+2), x2–5x+6 è divisibile per x–2 ma non per x+2; quindi m.c.d. = x–2, m.c.m.=(x+2)(x2–5x+6)

•  y = x2–6x+5 e y = x2–6x+8 sono parabole una immagine dell'altra mediante una traslazione verticale; quindi non possono avere intersezioni comuni con l'asse x e, perciò (teo. del resto), essere divisibili per uno stesso polinomio di 1° grado; quindi m.c.d. = 1 e m.c.m. = (x2–6x+5)(x2–6x+8).

•  Per x3–2x2+x–2 e x3–2x2+x+1 non si può ragionare come nel caso precedente: posso concludere che non sono divisibili per uno stesso polinomio di 1° grado, ma, a priori, potrebbero essere divisibili per uno stesso polinomio di 2° grado; usando l'algoritmo euclideo si ha:

(x3–2x2+x–2)/(x3–2x2+x+1) = 1 + – 3/(x3–2x2+x+1)

m.c.d.(x3–2x2+x–2, x3–2x2+x+1) = m.c.d.(3, x3–2x2+x+1) = 1 (intendendo m.c.d. standard)

quindi:  m.c.m. = (x3–2x2+x–2)·(x3–2x2+x+1)

(b)  Poiché il m.c.d. è 1 – vedi parte (a) – non possono essere divisibili per uno stesso polinomio di 1° grado e, quindi (t. del resto), azzerarsi sostituendo a x uno stesso numero. Si poteva concludere ciò anche direttamente osservando che le due figure sono una immagine dell'altra mediante una traslazione verticale: vedi i grafici a lato.

    Per altri commenti: funzioni polinomiali neGli Oggetti Matematici.

I calcoli possono essere controllati con WolframAlpha; esempio:
  gcd(x^3-2x^2+x-2, x^3-2x^2+x+1)

Per le operazioni tra polinomi vedi questo script.

   

Potevo anche usare R per affrontare i calcoli (magari in casi più complessi di questi): 

P=c(1,0,-4); Q=c(1,-5,6); solpol(reverse(P)); solpol(reverse(Q))
#  2    -2        (x-2)*(x+2)
#  2     3        (x-2)*(x-3)
P=c(1,-6,5); Q=c(1,-6,8); solpol(reverse(P)); solpol(reverse(Q))
#  1     5        (x-1)*(x-5)
#  2     4        (x-2)*(x-4)       non ci sono divisori comuni
#
P=c(1,-2,1,-2); Q=c(1,-2,1,1); solpol(reverse(P)); solpol(reverse(Q))
#  2                     (x-2)* ?
#  -0.46557123187677   (x+0.46..)* ?
divp( P, c(1,-2) )
# 1 0 0   1 -2   
#   1     0      STOP                    (x-2)*(x^2+1)
divp( Q, c(1, 0.46557123187677) )
# 1 0 0   -2.465571 1 1  
#   -2.465571 0   2.147899 1     
#     2.147899    -6.883383e-15  STOP    (x+0.46..)*(x^2-2.46..*x+2.14..)
# Non ci sono divisori comuni