(a)  Trasforma in frazione  x/(2x²−16x+30) + (2−x)/(3x²−30x+63)   [prima di fare altri calcoli vedi se puoi raccogliere a fattor comune degli atomi nei vari polinomi].

(b)  Risolvi rispetto a x l'equazione  x/(2x²−16x+30) + (2−x)/(3x²−30x+63) = 1.

(a)  Posso trovare il m.c.d. tra 2(x²–8x+15) e 3(x²–10x+21) usando l'algoritmo euclideo:
mcd(x²–8x+15, x²–10x+21) = mcd(x²–10x+21, 2x–6) = mcd(x²–10x+21, x–3) = mcd(x–3, –7x+21) = x–3.
Dall'ultima divisione ho trovato anche che x²–10x+21 = (x–3)(x–7).
Trovo poi, dividendo, che x²–8x+15 = (x–3)(x–5).
Quindi posso trasformare il termine iniziale in:
(3x(x–7)+2(2–x)(x–5)) / (2·3·(x–3)(x–5)(x–7)) = (3x(x–7)+2(2–x)(x–5)) / (6·(x²–8x+15)(x–7)) = … = (x²-7x-20) / (6(x³-15x²+71x-105))

Questo procedimento è in genere il più efficiente: ad es. se avessimo trovato subito che il m.c.d. è 1 non avremmo dovuto scomporre i due denominatori ma avremmo semplicemente preso come denominatore comune il loro prodotto. È possibile verificare la soluzione con WolframAlpha (basta ad es. battere gcd(x^2–8x+15, x^2–10x+21) per avere il m.c.d. tra i due polinomi indicati). In altre situazioni, in cui vi siano scomposizioni molto facili, si può ricorrere ad altre strategie.

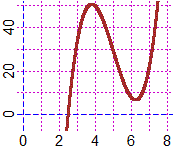
(b)  Per quanto fatto sopra mi riconduco all'equazione: x²-7x-20 = 6(x³-15x²+71x-105), ovvero a: 6x³-91x²+433x-610=0. Essendo una equazione di grado dispari ha sicuramente almeno una soluzione (siamo di fronte a una funzione continua che tande a −∞ e a ∞ per l'input che tende a −∞ e a ∞). Non appaiono evidenti scomposizioni che ci consentano di ricondurci facilmente a polinomi di grado più basso. Potrei tracciare il grafico col computer per capire che ha una sola soluzione ma posso procedere direttamente con uno script:

a = -10 b = 10     [...] a = 2.5280219735211835   b = 2.528021973521184 Posso concludere che 2.5280219735212 è la soluzione approssimata. Posso controllare con WolframAlpha: solve x/(2*x^2-16*x+30) + (2-x)/(3*x^2-30*x+63) = 1 x = 2.528021973521185288969229...     Per altri commenti: funzioni polinomiali neGli Oggetti Matematici.