2) Altra possibilità. Mi limito ad osservare che
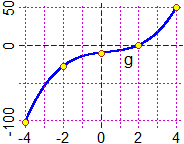
3) Col computer posso facilmente schizzare il grafico di g arrivare, in un attimo, alle stesse conclusioni.
4) Col computer posso facilmente trovare anche le soluzioni esatte. Vediamo come.
Trova, rapidamente, quante radici reali ha, rispetto all'incognita x, lequazione x4 x3 + 3x2 10x = 0.
A) nessuna B) una C) due D) tre E) quattro
x4 x3 + 3x2 10x = (x3 x2 + 3x 10)x
Una radice è 0 (escludo quindi la risposta A). Vediamo quante sono quelle di x3 x2 + 3x 10 = 0. Indichiamo con g(x) questo polinomio di grado 3
(essendo di grado 3 sicuramente ha almeno una soluzione, quindi le soluzioni dell'equazione inziale sono almeno 2: escludo la risposta B).
Possiamo procedere in vari modi.
1) Se conosco il concetto di derivata posso fare g'(x) = 3x2 2x + 3
che è sempre positivo (il discriminante è 2²−4·3·3 = −32, ossia negativo, per cui
2) Altra possibilità. Mi limito ad osservare che 3) Col computer posso facilmente schizzare il grafico di g arrivare, in un attimo, alle stesse conclusioni. 4) Col computer posso facilmente trovare anche le soluzioni esatte. Vediamo come. |  |
Usiamo questo script per studiare x3 x2 + 3x 10 = 0:

Con R (vedi qui) posso usare il comando "solpol":
solpol(c(0,-10,3,-1,1)) # 0 2Con WolframAlpha basta introdurre: solve x^4-x^3+3*x^2-10*x for x real