Risolvi rispetto a x l'equazione  5x(x–√3) = 1 / (x(x+√3))

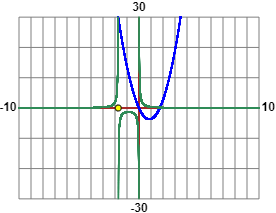
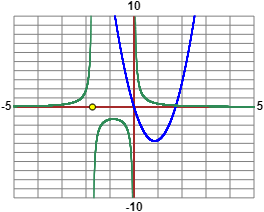
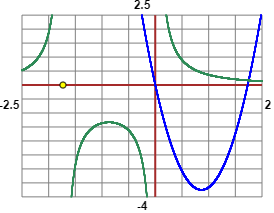
Schizzando i grafici di y=5x(x–√3) e y=1 / (x(x+√3)) si capisce che le soluzioni sono due (la parabola incontra l'altra curva nei pressi dell'asintoto sinistro, x = -√3):

   

[grafici ottenuti con questo script]

L'equazione è facilmente manipolabile moltiplicando i due membri per x(x+√3):
5x²(x–√3)(x+√3) = 1 AND x≠0 AND x≠√3
possiamo togliere le condizioni aggiunte in quanto 0 e √3 non sono evidentemente soluzioni:
5x²(x–√3)(x+√3) = 1
5x²(x²–3)–1 = 0   pongo u = x²:
u = x² AND 5u(u–3)–1 = 0
u = x² AND 5u²–15u–1 = 0 (risolvo l'eq. di 2° grado: )
u = x² AND (u = 1.5+√245/10 OR u = 1.5–√245/10);  poiché x²≥0:
u = x² AND u = 1.5+√245/10  da cui:
x = √(1.5+√245/10) = 1.750784848… OR x = –1.750784848…

Per risolvere l'equazione di 4º potevo anche ricorrere ad uno script per risolvere le equazioni polinomiali:

h = 5, p = -15, u = -1

a = 1   b = 2     [...]
a = 1.7507848480752433   b = 1.7507848480752435
a = -2   b = -1     [...]
a = -1.7507848480752435   b = -1.7507848480752433

-1.750784848075243 e 1.750784848075243 sono arrotondamenti delle soluzioni ultrasufficienti per ogni scopo pratico. Comunque posso risolvere l'equazione anche con WolframAlpha introducendo:
solve 5*x(x-sqrt(3)) = 1 / (x*(x+sqrt(3))) for x real
Ottengo:   x = ± sqrt(3/2 + 7/(2*sqrt(5))) = ± 1.750784848075243306960799…