Risolvi rispetto a x, usando le risorse che ritieni più opportune, l'equazione:
x⁵ - 7 x⁴ + 9 x³ + 9 x² - 7 x + 1 = 0

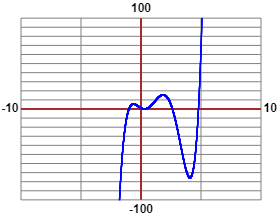
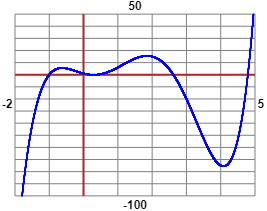
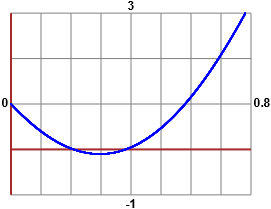
L'equazione polinomiale è di grado 5 (e quindi ha al massimo 5 soluzioni) e ha coefficiente direttivo > 0. Per x che tende a -∞ tende a -∞, per x che tende a ∞ tende a ∞. È evidente che -1 è una soluzione. Per affrontare il quesito conviene rappresentare la funzione polinomiale. Ecco che cosa si ottiene con questo script:

   

Dai grafici capisco che, oltre alla soluzione -1, ce ne sono una tra 0.1 e 0.3, una tra 0.3 e 0.5, una tra 2 e 3, una tra 4.5. Posso trovare, con ottima precisione, le soluzioni con lo script per risolvere le equazioni polinomiali:

a=0.1   b=0.3   [..]
a=0.20871215252208   b=0.20871215252208003
a=0.3   b=0.5   [..]
a=0.3819660112501051   b=0.38196601125010515
a=2   b=3
a=2.618033988749894   b=2.6180339887498945 a=4   b=5
a=4.79128784747792   b=4.791287847477921

Oltre ad 1, le soluzioni, arrotondate, sono 0.2087121525220800, 0.3819660112501051, 2.618033988749894, 4.79128784747792. Se copio ciascuno di questi numeri (tranne -1) in WolframAlpha ottengo:
    (5-sqrt(21))/2    2/(3+sqrt(5))    (3+sqrt(5))/2    (5+sqrt(21))/2.

Otterrei le soluzioni con WolpramAlpha anche introducendo:
solve x^5-7*x^4+9*x^3+9*x^2-7*x+1 = 0 for x real

In alternativa posso osservare che il polinomio si azzera per x=-1, e poi risolvere l'equazione che ottengo dividendo il polinomio per x+1, ottenendo x^4-8x^3+17x^2-8x+1. Posso affrontare x^4-8x^3+17x^2-8x+1 = 0 con qualche "trucco", recuperabile su qualche vecchio libro, trucco che potrebbe esistere, data la "simmetria" dei coefficienti. Il trucco c'è. Divido per x^2:
x^2 - 8x + 17 - 8/x + 1/x^2 = 0   raccolgo a fattor comune -8:
x^2 + 1/x^2 -8(x + 1/x) + 17 = 0   pongo u = x+1/x, da cui u^2 = x^2+1/x^2+2:
u^2 - 8u + 15 = 0 AND x^2 - ux + 1 = 0
(u = 3 OR u = 5) AND (x = u/2+√(u^2-4)/2 OR x = u/2-√(u^2-4)/2)
da cui ritrovo le soluzioni in forma simbolica trovate in precedenza.