Una pietra viene lanciata verso l'alto con velocità v e raggiunge l'altezza h, e si rilevano opportunamente h (in m) e v2 (in m2/s2) ottenendo i seguenti intervalli di indeterminazione:
| h | 0.4±0.05 | 0.8±0.05 | 1.4±0.05 | 2.0±0.05 | 2.6±0.05 | 3.4±0.05 | 3.8±0.05 |
| v2 | 7±3 | 17±3 | 25±3 | 38±4 | 46±5 | 62±5 | 72±6 |
Se sappiamo che l'accelerazione di gravità g (in m2/s) è legata a v ed h dalla relazione v2 = 2gh, quale intervallo di indeterminazione per g potremmo ricavare da questi valori?
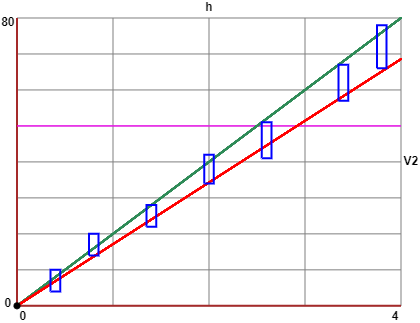
Riportiamo tali intervalli di indeterminazione sul piano cartesiano in cui scegliamo v2 ed h come variabili da associare ai due assi, ottenendo un grafico come il seguente:
Le rette di minima e massima pendenza che passano per (0,0) (l'unico punto certo)
e per tutti i rettangolini sono i grafici di x → 51/2.55·x
e di x → 66/3.85·x, da cui il valore di g (= v²/h/2), in m/s2,
è compreso tra 66/3.85/2 = 60/7 = 8.571428571428571 e 51/2.55/2 = 10,
ossia possiamo prendere g = 9.3±0.7 m/s2. Questo
è in accordo con i valori noti di g
(
vettori neGli Oggetti Matematici).
Potremmo fare i calcoli direttamente con WolframAlfha (vedi):
max {(7-3)/(0.4+0.05), (17-3)/(0.8+0.05), (25-3)/(14+0.05), (38-4)/(2+0.05),(46-5)/(2.6+0.05),(62-5)/(3.4+0.05),(72-6)/(3.8+0.05)}
(72 - 6)/(3.8 + 0.05)
(72 - 6)/(3.8 + 0.05)/2 = 8.57142857142... → 8.57
min {(7+3)/(0.4-0.05), (17+3)/(0.8-0.05), (25+3)/(14-0.05), (38+4)/(2-0.05),(46+5)/(2.6-0.05),(62+5)/(3.4-0.05),(72+6)/(3.8-0.05)}
(25 + 3)/(14 - 0.05)
(25 + 3)/(14 - 0.05) /2 = 1.0035842293906810035...→ 1.00
Il grafico è stato ottenuto con questo script.
Lo si può ottenere anche con R, ad es. con
queste istruzioni.