
| Ho la fotografia multiflash (uno scatto ogni 30-esimo di secondo) di una palla da biliardo lasciata cadere da una certa posizione, a fianco ad un metro graduato con tacche ampie un millimetro. Cliccando puoi ingrandire la foto (che per comodità è stata ruotata di 90°). Rappresenta graficamente il fenomeno e cerca di dedurne, con opportune elaborazioni, l'andamento (lo "0" del metro non corrisponde al punto esatto da cui è stata lasciata cadere la bilia). |
 |
Posso ritenere "esattamente" di 1/30 di secondo gli intervalli di tempo
tra uno scatto e il successivo, mentre devo valutare in modo opportunamente
approssimato le posizioni della pallina. Dalle foto riesco a valutare
le posizioni arrotondate al mezzo millimetro. Riferendosi alle posizioni
segnate con le tacche, individuandone le coordinate in centimetri, abbiamo:
9.5, 15, 21.5, 29.5, 38.5, 48.5, 59.5, 71.5, 85, 99, 114, 130.5, 148, 167
Facciamo i calcoli con R (vedi), ma potremmo usare altre risorse:
vedi qui (gli esempi) per l'impiego di script online, vedi più avanti per l'impiego del software online WolframAlpha.
Procediamo in due modi diversi.
# Primo.
source("http://macosa.dima.unige.it/r.R")
# Uso questa libreria per semplificare i comandi
p = c(9.5,15,21.5,29.5,38.5,48.5,59.5,71.5,85,99,114,130.5,148,167)/100
# ho espresso le posizioni in metri
n = length(p); n
[1] 14
n/30
[1] 0.4666667 n*1/30 Ŕ il tempo complessivo in sec
t = seq(0, 0.46, 1/30)
c( min(p), max(p) )
[1] 0.095 1.670
Plane(0,0.45, 0,1.7); POINT(t,p, "brown")
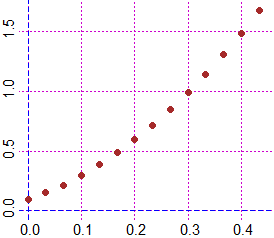
# Analizziamo come variano le "y", ossia le velocità:
j = 1:(n-1); v = (p[j+1]-p[j])/(t[j+1]-t[j])
c( min(v), max(v) )
[1] 1.65 5.70
# Scelgo la scala, e rappresento i punti (1 in meno), con le "x" a metÓ
# tra le precedenti (posiziono la pendenza media al centro degli intervalli)
Plane(0,0.45, 1.5,5.8)
POINT(t[1:13]+1/30/2,v[1:13], "brown")
# e traccio la retta approssimante:
regression1( t[1:13]+1/30/2, v[1:13] )
9.816 * x + 1.508
f = function(x) 9.816 * x + 1.508
graph1(f, 0,5, "blue")
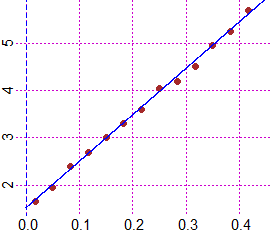
# La pendenza di questa retta è 9.8 (è la pendenza del grafico
# della velocità in funzione del tempo: l'accelerazione)
# Se so che la pendenza del grafico di una funzione polinomiale
# di 2° grado varia linearmente, posso dedurne che il fenomeno
# studiato ha andamento parabolico
# Secondo: trovare (con una cosiddetta "regressione del 2º ordine")
# la parabola che "meglio" approssima i punti
# tracciato il grafico come sopra:
Plane(0,0.45, 0,1.7); POINT(t,p, "brown")
regression2(t,p)
4.84 * x^2 + 1.54 * x + 0.0937
g = function(x) 4.84 * x^2 + 1.54 * x + 0.0937
graph1(g, 0,5, "blue")
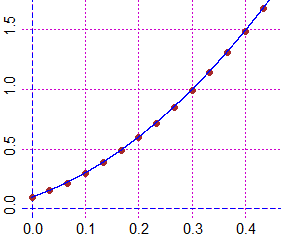
4.84*2
[1] 9.68
Esaminiamo i dati con WolframAlpha (vedi). Utilizziamo
i tempi in 30-esmi di secondo e lo spazio in centimetri.
quadratic fit {(0,9.5),(1,15),(2,21.5),(3,29.5),(4,38.5),(5,48.5),(6,59.5),(7,71.5),(8,85),(9,99),(10,114),(11,130.5),(12,148),(13,167)}
y = 0.537431 x^2 + 5.11669 x + 9.37321
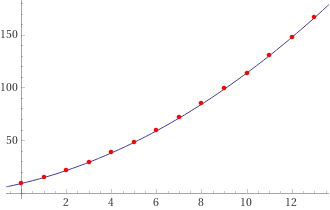
È ottima l'approssimazione con una funzione quadratica. Cambiamo unità di misura esprimendoci in metri (Y)
al secondo (X) quadrato. Ricordo che, data
Y = (0.537431 (X*30)^2 + 5.11669 X*30 + 9.37321)/100
Y = 0.537431*30^2/100*X^2 + 5.11669*30/100*X + 9.37321/100
Y = 4.836879*X^2 + 1.535007*X + 0.0937321
Il grafico precente andava tra 0 e 13, questo va tra 0 e 13/30
plot 4.836879*X^2 + 1.535007*X + 0.0937321, 0 < X < 13/30
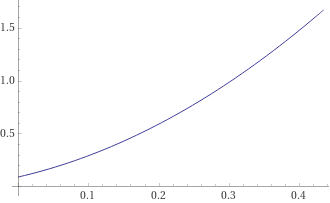
Abbiamo trovato, come sopra, il coefficiente direttivo 4.84.