Ho ipotizzato che un oggetto, quando viene collocato in un ambiente che ha una temperatura costante diversa dalla sua temperatura iniziale, tenda ad assumere la temperatura dell'ambiente con una rapidità di variazione che, istante per istante, si mantiene proporzionale alla differenza tra la temperatura dell'ambiente e la temperatura che esso ha in quell'istante. Per fare una verifica di questa ipotesi ho messo un termometro da forno in un forno, ho riscaldato il forno e, quando questo si è stabilizzato sulla temperatura di 145°C, ho estratto il termometro e l'ho collocato in un ambiente con temperatura di 20°C. Successivamente ho letto la temperatura del termometro (sul termometro stesso) ogni 30 s. Il grafico a lato (clicca sull'immagine per ingrandirlo) riporta gli esiti dei miei rilevamenti (in ascissa il tempo trascorso, in ordinata il salto tra temperatura ambiente e temperatura del termometro) tenendo conto della indeterminazione delle misure (legata, essenzialmente, alla graduazione del termometro): non ho segnato dei punti ma dei rettangolini.  Ecco, qui sotto, i valori delle temperature:
125,112,100,90,78,68,59,51,46,40,35,31,29,25,22,21,18, 16,14,12,11,10,10,9,8,7,6,6,5,4,4,3,2,1,1,1,1,1,1,1,0,0 		 
(1) Qual è la precisione con cui ho indicato le temperature?  (2) Gli esiti confermano la mia ipotesi?  (3) Descrivi mediante una formula matematica una funzione che approssimi l'andamento (dovrebbe essere quella che ha il grafico tracciato in modo punteggiato nella figura, e che passa per tutti i "rettangolini").  (4) Questo grafico tende a spiaccicarsi sull'asse orizzontale, ma non lo raggiunge mai. Vuol dire che l'oggetto non raggiungerà mai la temperatura ambiente?

Vedi più avanti come procedere col software online WolframAlpha con un numero minore di misure.

(1)  I rettangolini sono alti "4 °C". Quindi il primo rettangolino, che verticalmente va da 123° a 127°, rappresenta la temperatura 125±:2°; il secondo 112±:2°; …  Ecco come potrebbero essere tracciati i "punti" (con R, vedi), ottenendo la figura sotto riportata:

source("http://macosa.dima.unige.it/r.R")
tempo = seq(0,1230,30)
tempera = c(125,112,100,90,78,68,59,51,46,40,35,31,29,25,22,21,18,
          16,14,12,11,10,10,9,8,7,6,6,5,4,4,3,2,1,1,1,1,1,1,1,0,0)
length(tempera)
# 42     I punti sono 42
etempo=rep(2,100); etempera=rep(2,100)
BF=8; HF=4
Plane(0,1250, 0,130)
colRect="black"; pointDiff0(tempo,tempera,etempo,etempera)
abovex("s"); abovey("°C")
type(50,125,"°C"); type(1250,6,"s")

(2)  Possiamo, ad es., vedere se si mantiene costante il tempo di dimezzamento. Su vari esempi, vedi figura sotto a sinistra, si vede che questo è sempre di circa 175 s. (tra 170 e 180, ossia 175±5).
In alternativa possiamo osservare che il fatto che la velocità di variazione della temperatura abbia una relazione di tipo lineare con la temperatura ci fa concludere che la temperatura ha un andamento di tipo esponenziale rispetto al tempo. Possiamo precisare questa cosa analizzando i logaritmi delle temperature. Facciamolo usando il computer: 

lo=log(tempera)
min(lo[1:40]); max(lo[1:40])
#  0   4.828314
min(lo[1:41]); max(lo[1:41])
# -Inf   4.828314
Plane(0,1250, 0,5); Point(tempo,lo,"red")
# Ho ottenuto i pallini rossi, che approssimo poi col grafico di una funzione
POINT(tempo[1],lo[1],"brown"); POINT(tempo[21],lo[21],"brown")
r=(lo[21]-lo[1])/(tempo[21]-tempo[1]); r
# -0.004111241     la pendenza della retta che approssima i pallini:
# y = 4.828314 - 0.004111241*x    log(125) = 4.828314
f = function(x) lo[1]+r*x; graph1(f,0,1200,"blue")
#
# Ho un risultato simile trovando la retta di regressione (escludo gli ultimi punti)
regression(tempo[1:33],lo[1:33], 0,lo[1])
# -0.003965 * x + 4.828314
# prendo y = 4.83 - 0.0040 * x

Abbiamo visto che i punti, fino ad un certo punto, sono disposti più o meno lungo una retta (sui valori bassi la precisione relativa peggiora e non consente di avere informazioni attendibili). Abbiamo calcolato, approssimativamente, la pendenza di queste retta (r). Sopra abbiamo tracciato la retta che passa per il punto inziale e ha tale pendenza.

(3)  Ritorno al grafico iniziale operando con la funzione inversa di log: 

f = function(x) 4.83 - 0.0040 * x
h = function(x) exp(f(x))
BF=8; HF=4
Plane(0,1250, 0,130)
colRect="black"; pointDiff0(tempo,tempera,etempo,etempera)
abovex("s"); abovey("°C")
graph2(h,0,1250, "blue")

La funzione x → exp(4.83−0.0040*x) posso esprimerla come x → 125·exp(−0.004·x), in quanto 4.828314 non era altro che log(125). Volendo, dato che exp(-0.004*x) = u^x quando -0.004*x = x*log(u), ossia u = exp(-0.004) = 0.9960…, posso esprimerla anche come x → 125·0.996x

(4)  Tale funzione ha grafico (quello blu sopra raffigurato) che non arriva a toccare l'asse x, mentre la temperatura dell'oggetto prima o poi si stabilizza sul valore della tempeartura ambiente. Questa differenza non deve stupire: la funzione è un modello matematico che approssima il fenomeno reale, ma non coincide con esso. In particolare la temperatura di un corpo o di un ambiente a rigore non è rappresentabile esattamente con un numero reale: essa, infatti, corrisponde alla energia cinetica media della particelle, che fluttua, pur se con piccole oscillazioni, attorno ad un certo valore: l'oggetto raggiunge la temperatura ambientale quando le fluttuazioni della sua temperatura si interecano con quelle della temperatura dell'ambiente.
Per altro, questo modello rappresenta il fenomeno nell'ipotesi che anche nelle vicinanze dell'oggetto la temperatura sia quella ambientale mentre in realtà, se l'ambiente non è un po' ventilato, attorno al corpo si registra una temperatura leggermente maggiore, per cui, specie quando temperatura dell'oggetto e dell'ambiente sono molto vicine, il salto della temperatura effettivo ha una discerta differenza percentuale dal salto riferito alla temperatura ambientale "ufficiale"]
 

Suppongo di aver letto la temperatura del termometro ogni 60 s e di aver ottenuto le seguenti coppie (secondi,°C):
(0,125);(60,100);(120,78);(180,59);(240,46);(300,35);(360,29);(420,22);(480,18);(540,14);(600,11);(660,10);(720,8);(780,6);(840,5);(900,4);(960,2);(1020,1);(1080,1);(1140,1).
Rappresento graficamente questi dati utilizzando il software online www.wolframalpha.com (vedi qui).
plot {(0,125);(60,100);(120,78);(180,59);(240,46);(300,35);(360,29);(420,22);(480,18);(540,14);(600,11);(660,10);(720,8);(780,6);(840,5);(900,4);(960,2);(1020,1);(1080,1);(1140,1)}
Ottengo il grafico sotto a sinistra. Sembra aver andamento esponenziale. Verifco la cosa (ottengo il grafico sopra a destra):
exp fit {(0,125);(60,100);(120,78);(180,59);(240,46);(300,35);(360,29);(420,22);(480,18);(540,14);(600,11);(660,10);(720,8);(780,6);(840,5);(900,4);(960,2);(1020,1);(1080,1);(1140,1)}

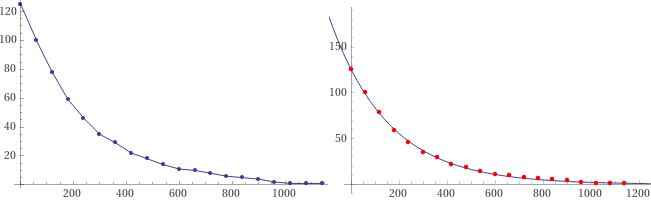
Il software mi dà anche l'equazione della funzione esponenziale:  125.764*e^(-0.00409652*x)

Poi vai al paragrafo (4).