Un peso sospeso alla estremità di una molla è tirato in giù di 4 cm dalla posizione di equilibrio e poi viene lasciato andare. Il periodo della oscillazione conseguente è di 3.5 s. Schizza il grafico, al passare del tempo, della posizione verticale del peso, della sua velocità e della sua accelerazione. Assumi come tempo inziale l'istante in cui per la prima volta il peso ripassa per la posizione inziale. Supponiamo che l'attrito sia trascurabile, per cui le prime oscillazioni abbiano la stessa ampiezza. Controlla la tua risposta con opportuno software.
La molla oscilla tra -4 e 4 con periodo 3.5 s. Il grafico
ha andamento sinusoidale. Indicando con y la quota in cm e con t il tempo in secondi,
assumendo come riferimento la posizione a riposo, abbiamo
La velocità, e quindi anche l'accelerazione, variano con lo stesso
periodo. Facendo i conti (derivata dello spazio in funzione del tempo, e derivata di questa
derivata) abbiamo che la velocità in cm/s è

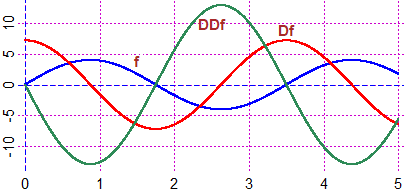
# I grafici (e i calcoli) con R (vedi) di s, s' e s" in funzione di t f = function(t) 4*sin(t*2*pi/3.5) Df = function(t) eval( deriv(f,"t") ) DDf = function(t) eval( deriv2(f,"t") ) graph2F(DDf, 0,5, "black") graph2(Df, 0,5, "brown") graph2(f, 0,5, "blue") # # I grafici, sovrapposti, di s' e s" calcolate "a mano" v = function(t) 2*pi*4/3.5*cos(2*pi*t/3.5) graph2(v, 0,5, "red") a = function(t) -(2*pi/3.5)^2*4*sin(2*pi*t/3.5) graph2(a, 0,5, "seagreen")
Usando il software online www.wolframalpha.com (vedi qui):
plot 4*sin(t*2*pi/3.5), D(4*sin(t*2*pi/3.5)), D(D(4*sin(t*2*pi/3.5))), 0 < t < 5
