∫ I x(1-x2)1/2dx = -1/3*(1-12)3/2+1/3*(1-02)3/2 = 1/3
1/3 = xB·π/4 xB = 1/3·4/π = 4/(3π) (=0.424…).
Più in generale, se R è il raggio del cerchio, il baricentro dista 4R/(3π) da entrambe le rette su cui stanno i raggi che delimitano la figura.

Determina il baricentro di una piastra di materiale omogeneo, di spessore costante, che ha la forma di un quarto di cerchio.
| Disponiamo un quarto di cerchio di raggio 1 nel modo illustrato a lato.
Per simmetria, la ordinta del baricentro coincide con la sua ascissa x.
Determiniamola. Il baricentro B è il punto in cui possiamo pensare concentrata tutta la massa per lo studio degli effetti rotatori.
Quindi il momento rispetto a (0,0) di una massa concentrata in esso equivale alla somma dei momenti dovuti alle striscette verticali in cui
possiamo pensare suddiviso il quarto di cerchio. Ragioniamo sull'aree in quanto le masse (nel caso di una piastra omogenea) sono ad esse proporzionali.
La striscetta di ampiezza dx e ascissa centrata in x ha area ∫ I x(1-x2)1/2dx = -1/3*(1-12)3/2+1/3*(1-02)3/2 = 1/3 1/3 = xB·π/4 xB = 1/3·4/π = 4/(3π) (=0.424…). Più in generale, se R è il raggio del cerchio, il baricentro dista 4R/(3π) da entrambe le rette su cui stanno i raggi che delimitano la figura. |
 |
| Potremmo fare il calcolo anche senza conoscere le tecniche di integrazione, ad esempio con dei semplici script (vedi l'esempio svolto nel link): | |
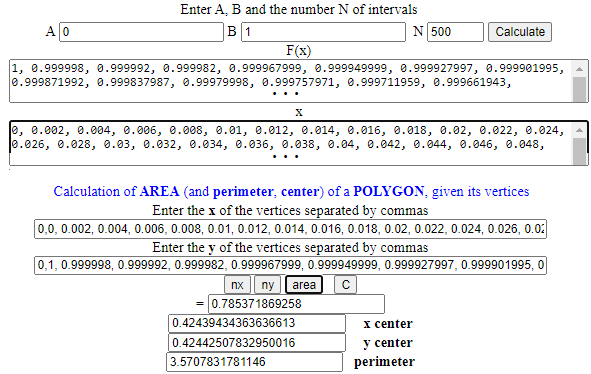
Posso prendere le coordinate (0.4244·R, 0.4244·R): l'arrtondamento a 4 cifre è più che sufficiente.
Si può fare il calcolo anche con software online www.wolframalpha.com. Vedi qui.
Calcolo e immagine con R (vedi).
source("http://macosa.dima.unige.it/r.R")
# Calcolo dell'integrale:
f = function(x) x*(1-x^2)^0.5
fraction(integral(f, 0,1))
# 1/3 da cui ricavo B
#
# Calcolo diretto approssimando il grafico con una polgionale.
# Grafico del quarto di cerchio
BF=2.5; HF=2.5; PLANE(0,1, 0,1)
g = function(x) sqrt(1-x^2); graph1(g, 0,1, "brown")
# Approssimo l'area sottesa con un poligono
x = seq(0,1, len=1e6); y = g(x); x=c(0,x,0); y=c(1,y,0)
polyC(x,y, "yellow")
# Il grafico si sovrappone. A questo punto calcolo il centroide
C = centerPol(x,y); C
# 0.4244132 0.4244132
POINT(C[1],C[2], "brown")
# Per provare a esprimere diversamente questo valore lo metto in WolframAlpha
# ottenendo 4/(π·3)
