Studia la convergenza di   ∫_[0,∞) x / √(x⁴+1) dx    ∫_(−∞,∞) e^−x2 dx    ∫_[0,∞) 1 / √(x³+1) dx    ∫_(0,∞) e^-√x / √x dx   (nota)

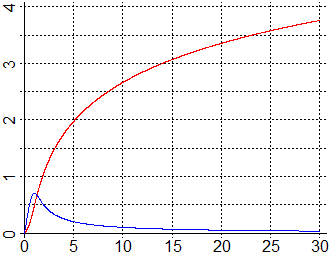
• Sotto sono tracciati il grafico (in blu) delle prima funzione da integrare e (in rosso) il grafico, al variare di x, dell'integrale tra 0 e x di essa.  Sono stati stampati anche i valori dell'integrale tra 0 ed 1, tra 1 e 10, tra 10 e 100, …, da cui si capisce che l'integrale tra 0 e ∞ della nostra funzione non converge.  (Grafico e calcoli sono fatti con R, ma si potrebbe usare un altro programma).

	F <- function(x) x/sqrt(x^4+1) integrate(F,0,1) # 0.4406868 with absolute error < 1.5e-13 integrate(F,1,1e1) # 2.208484 with absolute error < 6.3e-07 integrate(F,1e1,1e2) # 2.302573 with absolute error < 4.1e-05 integrate(F,1e2,1e3) # 2.302585 with absolute error < 4.1e-05 integrate(F,1e3,1e4) # 2.302585 with absolute error < 4.1e-05 # tra 1e4 e 1e5, tra …, sarà ancora 2.30…
plot(c(0,30),c(0,4),type="n") abline(v=seq(0,30,5),h=seq(0,4,1/2),lty=3); abline(v=0,h=0) a <- 0; b <- 30; x0 <- 0; n <- 5000 for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(F,x0,x)$value,pch=".",col="red") } curve(F,add=TRUE,col="blue",n=1000)

La conslusione è confermata dal fatto che l'integranda per l'input che va all'infinito è un infinitesimo di ordine 1 [vedi].

Come si può controllare il calcolo col software online WolframAlpha:

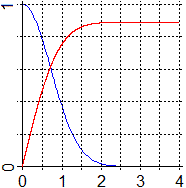
• Il successivo intergrale, ∫_(−∞,∞) e^−x2 dx, è di una funzione dal grafico simmetrico rispetto all'asse y.  Sotto sono tracciati il grafico (in blu) della funzione a destra dell'origine e (in rosso) il grafico, al variare di x, dell'integrale tra 0 e x di essa.  È evidente dal grafico che l'integrale improprio converge, e può essere calcolato in modo approssimato con R; del resto sappiamo già [ Leggi di distribuzione (continue)] che si tratta della funzione densità gaussiana moltiplicata per una costante.

F <- function(x) exp(-x^2) integrate(F, -Inf,Inf) # 1.772454 with absolute error < 4.3e-06 plot(F,0,4,col="blue") abline(v=seq(0,4,1/2),h=seq(0,1,1/5),lty=3); abline(v=0,h=0) a <- 0; b <- 4; x0 <- 0; n <- 5000 for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(F,x0,x)$value,pch=".",col="red") }

La conslusione è confermata dal fatto che l'integranda per l'input che va all'infinito è un infinitesimo di ordine più grande di un qualunque numero positivo [vedi].

Come si può controllare il calcolo col software online WolframAlpha:

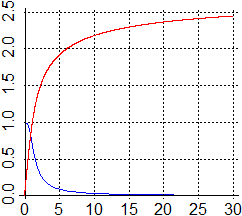
• Il terzo intergrale, ∫_[0,∞) 1 / √(x³+1) dx, è di una funzione di cui sotto (in blu) è tracciato il grafico, assieme a quello (in rosso) al variare di x, dell'integrale tra 0 e x di essa.  Sono riportati anche alcuni valori dell'integrale su successivi intervalli dai quali si capisce che l'integrale improprio converge; del resto si tratta dell'integrale di un infinitesimo (per l'input che tende all'infinito) di ordine 3/2 (> 1) rispetto ad 1/x [vedi].

F <- function(x) 1/sqrt(x^3+1) plot(F,0,30,ylim=c(0,2.5),col="blue") abline(h=seq(0,3,1/2),v=seq(0,30,5),lty=3); abline(v=0,h=0) a <- 0; b <- 30; x0 <- 0; n <- 5000 for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(F,x0,x)$value,pch=".",col="red") } integrate(F, 0,Inf) # 2.804364 with absolute error < 4e-05

Come si può controllare il calcolo col software online WolframAlpha:

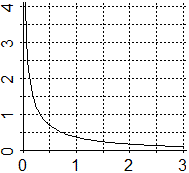
• L'ultimo intergrale, ∫_(0,∞) e^-√x / √x dx, è di una funzione che non è definita in 0, quindi dobbiamo studiare la convegenza sia dell'integrale tra 0 e, ad esempio, 1 che quella dell'integrale tra 1 e ∞.  Dagli esiti riportati sotto si capisce che entrambi gli integrali convergono.  Del resto siamo di fronte, per x → 0+, ad un infinito dello stesso ordine di 1/√x (infatti exp(x) tende ad 1), ossia di ordine 1/2 rispetto ad 1/x, e per x → ∞ ad un infinitesimo di ordine superiore rispetto a 1/xⁿ per ogni n numero naturale [vedi].

F <- function(x) exp(-sqrt(x))/sqrt(x) plot(F,0,3,ylim=c(0,4)); abline(v=0,h=0) abline(h=seq(0,4,1/2),v=seq(0,3,1/2),lty=3) integrate(F,0,Inf) # 2.000001 with absolute error < 0.00024 integrate(F,0,Inf,rel.tol=1e-10) # 2 with absolute error < 2.5e-11

Come si può controllare il calcolo col software online WolframAlpha:

I calcoli potrebberro essere effettuati anche con degli script: vedi.