|
È stato preso un cilindro graduato trasparente ed è stato posto sotto a un rubinetto facendo in modo che scenda un filo d'acqua.
Si rileva ogni 5 secondi il volume, in centilitri, raggiunto dall'acqua. Si ottengono i valori (approssimati) riportati a fianco.
Qual è, approssimativamente, la funzione che al tempo trascorso associa il volume dell'acqua via via uscita. | |
tempo (s) 0 5 10 15 20 25 30 35 40
volume (cl) 0 8 16 23 31 39 47 54 62 |
Si possono rappresentare i dati su carta quadrettata o millimetrata (vedi qui come ricuperarla),
ottenendo rappresentazioni simili a quella qui a fianco: | | 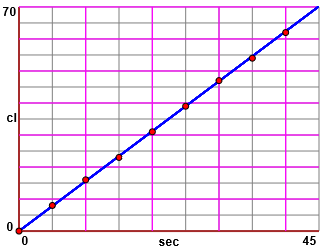 |
È evidente che per i punti (che rappresentano dati approssimati) passa all'incirca una semiretta che parte
dall'origine. Essa passa, circa, anche per il punto (45,70). 70/45 = 14/9 = 1.555… ≅ 1.56.
La funzione che al tempo trascorso in secondi associa il volume dell'acqua in centilitri è, approssimativamente:
x → 1.56·x
|
Volendo, poi, si può traccciare il grafico col computer. Il grafico precedente è
stato realizzato in JavaScript: vedi
Posso tracciare il grafico anche con WolframAlpha (vedi), mettendo più volte (0,0) in modo da imporre, più o meno, il passaggio per (0,0):
linear fit {(0,0),(0,0),(0,0),(0,0),(5,8),(10,16),(15,23),(20,31),(25,39),(30,47),(35,54),(40,62)}
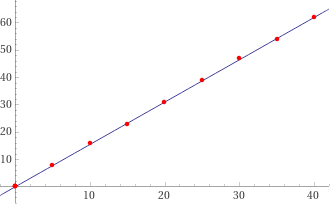
Alla fine delle superiori si possono utilizzare strumenti matematici più raffinati. Ecco come usare la regressione per trovare il coefficiente direttivo, 1.553 (vedi qui):

Ecco come procedere supponendo che i rilevamenti dei tempi abbiano la precisione di 1 secondo e i volumi di 0.5 centilitri.
I punti sperimentali sono rappresentati dai dei rettangolini con base ampia 2 (sec) e altezza ampia 1 (cl).
x: 5±1, 10±1, 15±1, 20±1, 25±1, 30±1, 35±1, 40±1
y: 8±1/2, 16±1/2, 23±1/2, 31±1/2, 39±1/2, 47±1/2, 54±1/2, 62±1/2.
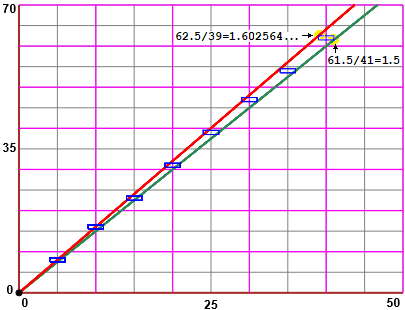 vedi qui
vedi qui
Indicata con F la funzione, abbiamo 1.5*x ≤ F(x) ≤ 1.602564*x, o più semplicemente
F(x) = (1.55±0.05)*x.
Potevo procedere anche impiegando R:
BF=5; HF=4
Plane(0,45,0,70)
ev = rep(0.5, 8)
es = rep(1, 8)
pointDif0(s,v, es, ev)
# Abbiamo ottenuto il grafico sotto a sinistra. Come ottenere quello a destra:
pointDif(0,0, s,v, es, ev)
# 1.5 * x 1.602564 * x f(x) sta tra questi valori
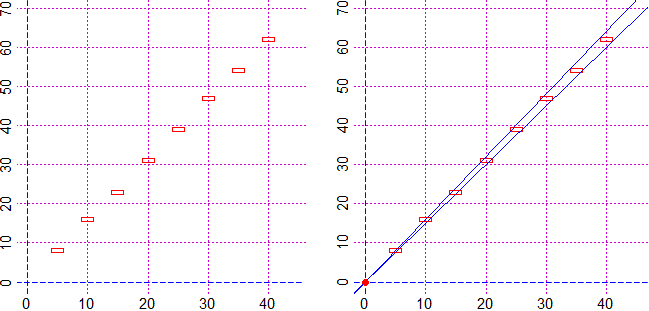



 vedi qui
vedi qui