| Studia i limiti per x → − 2 di |
x3+x2−8x−12 |
, |
x3+3x2−10x−24 |
e |
x2−3x−10 |
| —————— |
——————— |
—————— |
| x2−3x−10 |
x2−3x−10 |
x3+x2−8x−12 |
|
In tutti i tre i casi si tratta di rapporti tra termini che per x = −2 si annullano.
Quindi ho delle forme del tipo "0/0", di fronte alle quali non posso stabilire direttamente
il comportamento della funzione per x → − 2. Si tratta, comunque,
di polinomi in x, per cui, per il teorema del resto (di Ruffini) so che posso dividerli esattamente per x+2. Eseguo,
dunque, le loro divisioni per x+2, ottenendo: |
| x3+x2−8x−12 |
= x2−x−6 |
| —————— |
| x + 2 |
|
|
| x3+3x2−10x−24 |
= x2+x−12 |
| ——————— |
| x + 2 |
|
|
| x2−3x−10 |
= x−5 |
| ————— |
| x + 2 |
|
|
Dunque: |
| x3+x2−8x−12 |
= |
x2−x−6 |
→ 0/-7 = 0 |
| —————— |
———— |
| x2−3x−10 |
x−5 |
|
| x3+3x2−10x−24 |
= |
x2+x−12 |
→ 10/7 |
| ——————— |
———— |
| x2−3x−10 |
x−5 |
|
| x2−3x−10 |
= |
x−5 |
→ "-7/0" = ? |
| —————— |
———— |
| x3+x2−8x−12 |
x2−x−6 |
|
Per l'ultimo limite dobbiamo stabilire se, per x→-2, x2−x−6
tende a 0 mantenendosi positivo o negativo. y=x2−x−6
è una parabola con la concavità verso l'alto che interseca l'asse x
per x=-2 e per x=3 (infatti (x2−x−6)/(x+2) = x-3)
quindi tra x=-2 e x=3 sta sotto all'asse x ed esternamente sta sopra. Dunque:
per x→-2- x2−x−6>0 e il limite è
"-7/0+" = −∞
per x→-2+ x2−x−6<0 e il limite è
"-7/0-" = ∞ |
Verifica: calcolo il rapporto per -2.01 (a sinistra di -2) e ottengo -139.9...;
calcolo il rapporto per -1.99 (a destra di -2) e ottengo 140.0.... OK
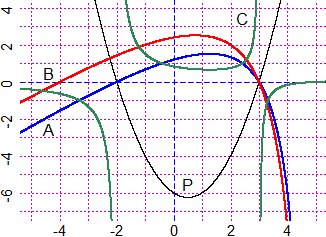
Controllo grafico al computer (a destra A, B e C sono, in ordine, i grafici delle tre funzioni;
P è il grafico della parabola y=x2−x−6):
|
 |
Volendo, i limiti sono facili da studiare anche con la calcolatrice. L'unico un po' complicato è il secondo.
Usando la nostra calcolatrice (vedi):

mettendo il termine con Q al posto di x in d e mettendo
in g valori man mano più vicini a -2:
(pow(Q,3)+3*pow(Q,2)-10*Q-24) / (pow(Q,2)-3*Q-10)
-1.99999, -1.999999, -1.9999999, -1.99999999, -1.999999999
clicco [F] e
in k ottengo:
1.4285777550644743, 1.4285720618246063, 1.428571490200136, 1.428571472074046, 1.4285714285714286
Il limite è dunque 1.42857142857142857... Per trovare la frazione equivalente posso utilizzare
questo altro script ottenendo 10/7.

# Posso verificare gli esiti col computer anche con R - vedi):
source("http://macosa.dima.unige.it/r.R")
f = function(x) (x^3+x^2-8*x-12)/(x^2-3*x-10)
g = function(x) (x^3+3*x^2-10*x-24)/(x^2-3*x-10)
h = function(x) (x^2-3*x-10)/(x^3+x^2-8*x-12)
k = function(x) x^2-x-6
BF=4; HF=3; Plane(-5,5, -7,4)
graph1(k, -6,6, "black")
graph2(f, -6,6, "blue"); graph2(g, -6,6, "red"); graph2(h, -6,6, "seagreen")
text(0.5,-5.5,"P")
text(-4.4,-2.5,"A"); text(-4.4,0.5,"B"); text(2.4,3.5,"C")
#
n = 1:10
x = -2+10^-n; more(g(x))
# 1.49130434782608 1.43489270386265 1.42920402914657 1.42863469335316 1.42857775506447
# 1.42857206182461 1.42857149020014 1.42857147207405 1.42857142857143 1.42857142857143
fraction(g(x))
# 343/230 33433/23300 29983177/20978934 5387380/3770999 10/7
# 10/7 10/7 10/7 10/7 10/7


