Sia f: x → sin(10x) + cos(3x). Trovare, usando opportunamente R o altro software, senza calcolare derivate,
il valore massimo di f e i valori in cui f assume tale valore.
Per l'uso di R, vedi.
source("http://macosa.dima.unige.it/r.R")
f = function(x) sin(10*x)+cos(3*x)
BF=5; HF=2.5
graph2F( f, -1,13, "brown")
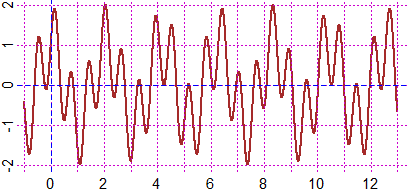 ## e' evidente che il periodo e' 6.28… = 2*pi; verifica grafica:
graph2( f, 0,2*pi, "blue"); coldash="yellow"; graph2( f, 0,2*pi, 0)
## e' evidente che il periodo e' 6.28… = 2*pi; verifica grafica:
graph2( f, 0,2*pi, "blue"); coldash="yellow"; graph2( f, 0,2*pi, 0)
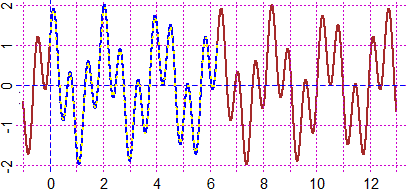 ## e numerica:
f(3); f(3+2*pi)
# -1.899162 -1.899162
#
## Capisco che il massimo e' intorno a 2. Posso trovarlo con successivi zoom:
graph2F(f, 1.8, 2.2, "brown")
## e numerica:
f(3); f(3+2*pi)
# -1.899162 -1.899162
#
## Capisco che il massimo e' intorno a 2. Posso trovarlo con successivi zoom:
graph2F(f, 1.8, 2.2, "brown")
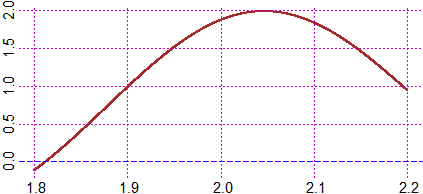 # ...
## Ma posso piu' semplicemente usare il comando "maxmin"
maxmin(f, 1.8,2.2)
# 2.046346
f( maxmin(f,1.8,2.2) )
# 1.9887
## I punti di massimo sono 2.046346 + 2*n*pi con n intero
## Posso verificare la cosa con WolframAlpha, battendo max of sin(10*x)+cos(3*x)
## e period of sin(10*x)+cos(3*x)
# ...
## Ma posso piu' semplicemente usare il comando "maxmin"
maxmin(f, 1.8,2.2)
# 2.046346
f( maxmin(f,1.8,2.2) )
# 1.9887
## I punti di massimo sono 2.046346 + 2*n*pi con n intero
## Posso verificare la cosa con WolframAlpha, battendo max of sin(10*x)+cos(3*x)
## e period of sin(10*x)+cos(3*x)
Il grafico, migliore, realizzato con questo script:
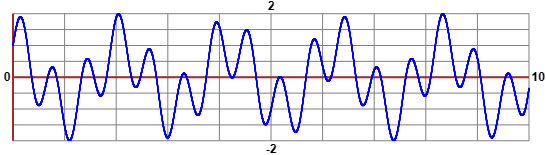
Potrei fare facilmente (e con più precisione) tutti i calcoli con questa calcolatrice online (vedi).
• Tabulo la funzione per trovare il punto di minimo che è intorno ad 1:
sin(10*Q)+cos(3*Q)
0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5
F(data):
-0.8881870729954355, -0.5066175928920127, 0.15214049411893193, 0.251964531082136, -0.4919536567753046, -1.5340136074898152, -1.9874699764595682, -1.4333313343345822, -0.30576526737349896, 0.5003465343541702, 0.43949204072633713
• Il minimo è tra 1 e 1.2. Usando [m] ne preciso il valore:
Metto in a e b 1 1.2 e clicco più volte [m]:
Q= 1.0666666666666667 dif= 0.1333333333333333 F(Q)= -1.9274941761139037
...
Q= 1.0952466387052955 dif= 1.2058363640932157e-8 F(Q)= -1.9886997585349235
Q= 1.0952466366955682 dif= 8.038909093954771e-9 F(Q)= -1.9886997585349238
Q= 1.0952466353557502 dif= 5.359272803318049e-9 F(Q)= -1.9886997585349242
Q= 1.0952466362489623 dif= 3.572848461530498e-9 F(Q)= -1.9886997585349242
F(Q) si è stabilizzato. Q è tra i due ultimi valori. Prendo
1.09524664 dove F vale -1.988699758534924
[ con più precisione potrei trovare 1.095246636318383 ]
• Tabulo la funzione per trovare il punto di massimo che è intorno ad 2:
1.5, 1.6, 1.7, 1.8, 1.9, 2, 2.1, 2.2, 2.3, 2.4, 2.5
F(data):
0.43949204072633713, -0.20040433322561801, -0.5834197491665766, -0.11629437082904148, 0.9845899945021117, 1.8731155373779935, 1.8365142749194712, 0.9413812826681254, -0.030495304049813265, -0.29722704747436857, 0.2142835677372528
Metto in a e b 1.9 2.2 e clicco più volte [M]:
Q= 2 dif= 0.20000000000000018 F(Q)= 1.8548149061487322
...
Q= 2.046346020690665 dif= 2.713131808107505e-8 F(Q)= 1.988699758534921
Q= 2.046346016168779 dif= 1.808754523935363e-8 F(Q)= 1.9886997585349224
Q= 2.0463460191833693 dif= 1.2058363640932157e-8 F(Q)= 1.9886997585349238
Q= 2.0463460171736423 dif= 8.038909093954771e-9 F(Q)= 1.9886997585349238
F(Q) si è stabilizzato. Q è tra i due ultimi valori. Prendo
2.04634602 dove F vale 1.988699758534924
[ con più precisione potrei trovare 2.046346017271411 ]
Ovviamente se il problema fosse in qualche modo di tipo applicativo basterebbe conoscere le soluzioni con minore precisione.
 ## e' evidente che il periodo e' 6.28… = 2*pi; verifica grafica:
graph2( f, 0,2*pi, "blue"); coldash="yellow"; graph2( f, 0,2*pi, 0)
## e' evidente che il periodo e' 6.28… = 2*pi; verifica grafica:
graph2( f, 0,2*pi, "blue"); coldash="yellow"; graph2( f, 0,2*pi, 0)
 ## e numerica:
f(3); f(3+2*pi)
# -1.899162 -1.899162
#
## Capisco che il massimo e' intorno a 2. Posso trovarlo con successivi zoom:
graph2F(f, 1.8, 2.2, "brown")
## e numerica:
f(3); f(3+2*pi)
# -1.899162 -1.899162
#
## Capisco che il massimo e' intorno a 2. Posso trovarlo con successivi zoom:
graph2F(f, 1.8, 2.2, "brown")
 # ...
## Ma posso piu' semplicemente usare il comando "maxmin"
maxmin(f, 1.8,2.2)
# 2.046346
f( maxmin(f,1.8,2.2) )
# 1.9887
## I punti di massimo sono 2.046346 + 2*n*pi con n intero
## Posso verificare la cosa con WolframAlpha, battendo max of sin(10*x)+cos(3*x)
## e period of sin(10*x)+cos(3*x)
# ...
## Ma posso piu' semplicemente usare il comando "maxmin"
maxmin(f, 1.8,2.2)
# 2.046346
f( maxmin(f,1.8,2.2) )
# 1.9887
## I punti di massimo sono 2.046346 + 2*n*pi con n intero
## Posso verificare la cosa con WolframAlpha, battendo max of sin(10*x)+cos(3*x)
## e period of sin(10*x)+cos(3*x)
