Batti sulla calcolatrice un qualunque numero positivo e premi ripetutamente il tasto  (in qualche modello, ad es. nella calcolatrice scientifica incoporata in Windows, occorre premere
(in qualche modello, ad es. nella calcolatrice scientifica incoporata in Windows, occorre premere 
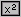 , ossia selezionare la radice quadrata come "inversa" dell'elevamento al quadrato; in altri modelli, in cui si possono scrivere sul visore più numeri ed operazioni, occorre prima premere
, ossia selezionare la radice quadrata come "inversa" dell'elevamento al quadrato; in altri modelli, in cui si possono scrivere sul visore più numeri ed operazioni, occorre prima premere  e poi introdurre il numero). Oppure realizza un programma che dato un numero in input applichi a questo la radice quadrata, poi la riapplichi all'output, poi al nuovo output, e così via, stampando man mano gli output ottenuti.
e poi introdurre il numero). Oppure realizza un programma che dato un numero in input applichi a questo la radice quadrata, poi la riapplichi all'output, poi al nuovo output, e così via, stampando man mano gli output ottenuti.
Che cosa osservi? Sai esprimere il fenomeno osservato usando opportunamente il simbolo "lim"?
Ecco gli output che si succedono con una CT a 8 cifre se si parte da 2 o da 0.3. Esiti simili si ottengono con qualsiasi altro numero positivo. In tutti i casi l'output si stabilizza su 1, o, per problemi di arrotondamento della CT, su un numero che differisce di una o due unità sull'ultima cifra.
2 1.4142136
1.1892071
1.0905077
1.0442738
1.0218972
1.0108893
1.0054299
1.0027113
1.0013547
1.0006771
1.0003385
1.0001692
1.0000846
1.0000423
1.0000211
1.0000105
1.0000052
1.0000026
1.0000013
1.0000006
1.0000003
1.0000001
1.0000001 …
0.3
0.54772256
0.74008281
0.86028066
0.92751316
0.96307485
0.98136377
0.99063806
0.99530802
0.99765125
0.99882493
0.99941229
0.9997061
0.99985304
0.99992652
0.99996326
0.99998163
0.99999081
0.9999954
0.9999977
0.99999885
0.99999942
0.99999971
0.99999985
0.99999992
0.99999996
0.99999998
0.99999999
1
1 …
Se indichiamo con x(.) la successione dei valori man mano visualizzati dalla CT, ossia la successione:
x(0) = "numero battuto inizialmente", x(1) = "numero ottenuto premendo 1 volta  ", x(2) = "numero ottenuto premendo 2 volte
", x(2) = "numero ottenuto premendo 2 volte  ", …
", …
possiamo descrivere il fenomeno con:
| lim x (n) | = 1 |
n →  |
Una descrizione più formale della successione può essere la seguente, dove k è il numero battuto inizialmente:
x(0) = k AND x(n+1) =  x(n)
x(n)
Con R, ad es. nel caso di k = 1/7, potremmo semplicemente
procedere così:
x = 1/7; for(n in 0:25) {x = sqrt(x); print(x)}
per ottenere: 0.3779645 0.6147882 ... 0.9999998 0.9999999 1 1
Per altri commenti:  successioni e limiti neGli Oggetti Matematici.
successioni e limiti neGli Oggetti Matematici.
Senza usare una calcolatrice potrei usare questo semplice script:

rad(1.0001692397053021) = 1.0000846162726942
rad(1.0003385080526823) = 1.0001692397053021
rad(1.0006771306930664) = 1.0003385080526823
rad(1.0013547198921082) = 1.0006771306930664
rad(1.0027112750502025) = 1.0013547198921082
rad(1.0054299011128027) = 1.0027112750502025
rad(1.0108892860517005) = 1.0054299011128027
rad(1.0218971486541166) = 1.0108892860517005
rad(1.0442737824274138) = 1.0218971486541166
rad(1.0905077326652577) = 1.0442737824274138
rad(1.189207115002721) = 1.0905077326652577
rad(1.4142135623730951) = 1.189207115002721
rad(2) = 1.4142135623730951
Col software online WolframAlpha:
x(1) = 1/7, x(n+1) = sqrt(x(n))

x(1) = 2, x(n+1) = sqrt(x(n))

 (in qualche modello, ad es. nella calcolatrice scientifica incoporata in Windows, occorre premere
(in qualche modello, ad es. nella calcolatrice scientifica incoporata in Windows, occorre premere 
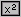 , ossia selezionare la radice quadrata come "inversa" dell'elevamento al quadrato; in altri modelli, in cui si possono scrivere sul visore più numeri ed operazioni, occorre prima premere
, ossia selezionare la radice quadrata come "inversa" dell'elevamento al quadrato; in altri modelli, in cui si possono scrivere sul visore più numeri ed operazioni, occorre prima premere  e poi introdurre il numero). Oppure realizza un programma che dato un numero in input applichi a questo la radice quadrata, poi la riapplichi all'output, poi al nuovo output, e così via, stampando man mano gli output ottenuti.
e poi introdurre il numero). Oppure realizza un programma che dato un numero in input applichi a questo la radice quadrata, poi la riapplichi all'output, poi al nuovo output, e così via, stampando man mano gli output ottenuti.
 x(n)
x(n)



