infiniti e infinitesimi

Dimostra che, per x → 0,	2^x – 1	→ log(2)	sapendo che (exp(x)-1)/x → 1
	————
	x

Cerco di ricondurmi il primo termine del rapporto alla forma exp(t)-1.
Idea: usare il fatto che exp e log sono una l'inversa dell'altra [u = exp(log(u))] e le loro proprietà:

2^x – 1	=	exp(log(2^x)) – 1	=	exp(x·log(2)) – 1	=	exp(x·log(2)) – 1	log(2) → 1·log(2)
———		———————		———————		———————
x		x		x		x·log(2)

Facciamo, comunque, una verifica anche numerica; qui usiamo la nostra calcolatrice (vedi):

mettendo il termine con Q al posto di x in d e mettendo in g valori man mano più vicini a 0:

( pow(2,Q)-1 ) / Q
1e-2,1e-4,1e-6,1e-8
clicco [F] e in k ottengo:
0.6955550056718884, 0.6931712037649973, 0.6931474207938493, 0.6931471840943004
Mettendo log(2) in d e cliccando [=] ottengo:
log(2) = 0.6931471805599453

Verifica con WolframAlpha:

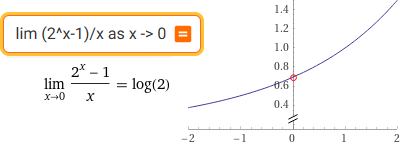
# verifica con R (vedi):

source("http://macosa.dima.unige.it/r.R")
f = function(x) (2^x-1)/x
BF=3; HF=3
Plane( -2,2, 0,f(2) )
graph(f, -2,2, "brown")
x=10^-(1:14); f(x)
#  0.7177346 0.6955550 0.6933875 0.6931712 0.6931496 0.6931474 0.6931472
#  0.6931472 0.6931471 0.6931478 0.6931566 0.6932233 0.6927792 0.6883383
#  Dopo che le uscite si sono stabilizzate su 0.6931472 intervengono errori
#  di approssimazione.   Prendo 0.6931472.   Verifica:
log(2)
#  0.6931472    OK