• x³+ y³- xy = 0 è il grafico di una funzione?
• Quali sono le rette tangenti ad essa nei suoi punti di intersezione con le rette y=x e y=x/2?

• Anche senza provare a tracciarla, capiamo che F(x,y) = x³+ y³- xy = 0 non può essere il grafico y=g(x) di una funzione continua g:
# è simmetrica rispetto alla retta y=x (se scambio x con y ottengo una equazione equivalente);
# passa per il punto (0,0) (la coppia (x,y)=(0,0) è soluzione dell'equazione) ed interseca y=x in un unico ulteriore punto (2x^3=x^2 anche per x=1/2);

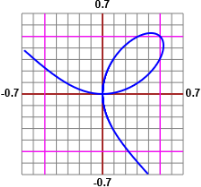
e quindi deve avere un aspetto del tipo di quello a fianco, ossia essere una curva che tra i due punti forma una specie di anello.     In ogni caso, preso un x compreso tra 0 e 1/2, è facile verificare che l'equazione risolta rispetto a y ha due soluzioni.     Sotto a sinistra è rappresentata parzialmente la curva così come la si ottiene con una fitta tabulazione (a mano o col computer).

• Troviamo le tangenti alla curva nei punti di intersezione con y=x, ossia in O = (0, 0) e in A = (1/2, 1/2), e con y=x/2, ossia in B = (4/9, 2/9) (infatti x^3+x^3/8-x^2/2 = 0 per x=4/9).     Non trattandosi del grafico di una funzione non possiamo fare semplicemente delle derivate. Possiamo procedere in due modi, cercando di ricondurci o al caso di curve descrivibili come y=g(x) o a quello di curve descritte come (x,y) = (h(t),k(t)).     Vediamo entrambi questi metodi, anche se, tenendo conto del grafico schizzato e della simmetria della curva, potremmo dedurre come sono le tangenti in O e in A.

1° modo.  Per trovare la pendenza della tangente a F(x,y)=0 in P ipotizzo che G sia una funzione derivabile che in un intorno di P abbia grafico y=G(x) coincidente con la curva F(x,y)=0, ossia che, intorno a P, F(x,G(x)) = 0.
    Derivando F(x,G(x)) ottengo:
D_x(x³+ G(x)³ - xG(x)) = 3x² + 3 G(x)²G'(x) - (G(x)+xG'(x)) = 0, da cui:
G'(x) = (3x² - G(x)) / (x - 3 G(x)²) = (3x²-y) / (x-3y²)
    Per P = A = (1/2,1/2) la tangente ha pendenza G(1/2) = (3(1/2)²-1/2) / (1/2-3(1/2)²) = -1, ed ha quindi equazione y = -1(x-1/2)+1/2, ossia y = -x + 1.
    Per P = O questo metodo non funziona, in quanto intorno ad O non posso confondere la curva col grafico di un'unica funzione: in O la curva ha un "nodo". Del resto otterrei G'(x) = 0/0.
    Per P = B = (4/9/2/9) la tangente ha pendenza G(4/9) = (3(4/9)²-2/9) / (4/9-3(2/9)²) = 11/8, ed ha quindi equazione y = 11(x-4/9)/8+2/9, ossia y = 11/8x-7/18

2° modo.  Ipotizzo che x=h(t), y=k(t) (con h e k derivabili) sia una descrizione alternativa della curva F(x,y)=0.     Derivando F(h(t),k(t)) ottengo: Dt(h(t)3+k(t)3 - h(t)k(t)) = 3h(t)2h'(t) + 3k(t)2k'(t) - (h'(t)k(t)+h(t)k'(t)) = 0, da cui. h'(t) (3x2-y) + k'(t) (3y2-x) = 0 (h'(t), k'(t)) è un vettore diretto come la tangente in P = (h(t), k(t)). Da  h'(t) (3x2-y) + k'(t) (3y2-x) = 0  segue che  k'(t)/h'(t) = -(3x2-y)/(3y2-x), ovvero che  (h'(t), k'(t)), e quindi la tangente, è diretta come  (-(3y2-x), 3x2-y).     Per P = A = (1/2,1/2) riottengo che la pendenza è k'(t)/h'(t) = -(3(1/2)2-1/2) / (3(1/2)2-1/2) = -1. Anche per B riottengo la stessa pendenza trovata sopra. E anche per O ritrovo quanto ottenuto sopra, ossia che non è individuabile la direzione della tangente: sarebbe diretta come il vettore (0,0), che non ha direzione.     Per individuare le tangenti in O dovremmo esplicitare una descrizione della curva come x=h(t), y=k(t), trovare i valori t1 e t2 di t a cui corripondono i due "passaggi" della traiettoria per O e calcolare (h'(t1), k'(t1)) e (h'(t2), k'(t2)).

Il grafico precedente è stato realizzato con questo script.

Nota 1.  Questa curva si chiama folium di Cartesio e una sua descrizione parametrica è x=h(t)=t/(1+t³), y=k(t)=t²/(1+t³). Passa in O per t=0 e tende a raggiungerlo per t → ∞ (o t → -∞). Abbiamo (h'(0), k'(0)) = (1, 0) (questa tangente è diretta come l'asse x: vedi figura). L'altra tangente la possiamo determinare sfruttando la simmetria rispetto a y=x: deve essere diretta come l'asse y.
Nota 2.  Se si conosce il calcolo differenziale per le funzioni di più variabili, si può osservare che il metodo 2 equivale a calcolare il gradiente di F e ad usare il fatto che il prodotto scalare del gradiente (che ha direzione perpendicolare alle curve del tipo F(x,y)=k) e un vettore (a,b) tangente alla curva deve essere nullo. Ad es. nel caso della nostra curva abbiamo:
Grad(F)(x,y)·(a,b) = (3x²-y, 3y²-x)·(a,b) = a(3x²-y) + b(3y²-x) = 0
per cui il vettore (a,b) tangente in (x,y) alla curva deve essere proporzionale a (-(3y²-x), 3x²-y), ossia a (-∂F(x,y)/∂y, ∂F(x,y)/∂x)).

# Come si puņ procedere con R (vedi; cerca "tangente" nell'indice per temi)
source("http://macosa.dima.unige.it/r.R")
H = function(x,y) x^3+y^3-x*y
BF=3; HF=3; PLANE(-1,1, -1,1); CURVE(H, "brown")
#
f=function(x) x; g=function(x) x/2
graph1(f,-1,1, "red"); graph1(g,-1,1, "red")
# intersezione x^3+y^3-x*y = 0 & y = x
Q = function(x) x^3+x^3-x*x; solution(Q,0, 0.3,0.51)
# 0.5   Il punto "blu":
POINT(0.5,0.5, "blue")
point_inclina(0.5,0.5, -45, "blue" )
# intersezione x^3+y^3-x*y = 0 & y = x/2
Q = function(x) x^3+(x/2)^3-x*x/2; solution(Q,0, 0.4,0.5)
# 0.4444444
fraction(last())
# 4/9
# Trovo la y corrispondente
k = function(y) H(4/9, y); solution(k,0, 0.2,0.3)
# 0.2222222
fraction(last())
# 2/9   Il punto "verde":
POINT(4/9,2/9,"seagreen")
# vettore perpendicolare alla curva nel punto (x,y)
c( deriv(H,"x"), deriv(H,"y") )
#  3 * x^2 - y    3 * y^2 - x
# vettore tangente (č perpendicolare al precedente)
#  -3*y^2+x    3*x^2-y
# In  4/9, 2/9
fraction( c(-3*(2/9)^2+4/9, 3*(4/9)^2-2/9) )
# 8/27 10/27
point_inclina(4/9,2/9, dirArrow1(0,0, 8/27, 10/27), "seagreen" )