Si consideri la successione	a: n →	(n + n·(−1)n)·e−n
		———————
		n2 + 1

(1) Stabilire se la successione è crescente, decrescente o né l'una cosa né l'altra.
(2) Determinare l'estremo inferiore e quello superiore di {a(n) / n intero non negativo}
(3) Stabilire se esiste (ed eventualmente calcolare) lim _{n → ∞} a(n)

(1) Per n dispari a(n) = 0. Per n pari a(n) = 2n·e⁻ⁿ/(n²+1), che è positivo per n > 0. Quindi a(n) alterna numeri nulli a numeri positivi: non è né crescente né decrescente.
(2) L'estremo inferiore, ed anche minimo, di {a(n) / n intero non negativo} è 0, in quanto 0 valgono i termini di indice dispari e gli altri non sono negativi.
(3) e^N per N → ∞ va all'infinito (più velocemente di qualsiasi polinomio in N), quindi per N pari  a(N) = 2N/(N²+1)/e^N → 0/∞ = 0.
Per N dispari a(N) = 0.
Quindi per N → ∞  a(N) → 0.

La conferma degli esiti usando questa calcolatrice.

(M+M*pow(-1,M))*exp(-M) / (M*M+1)
M = 1  -> 0     M = 2  -> 0.10826822658929017
M = 3  -> 0     M = 4  -> 0.008619124182933731
M = 5  -> 0     M = 6  -> 0.0008039196248647649
M = 7  -> 0     M = 8  -> 0.00008257541609907984
M = 9  -> 0     M= 10  -> 0.000008990085101482148
M= 11  -> 0     M= 12  -> 0.0000010169730791715657

La conferma degli esiti usando il programma R (vedi).

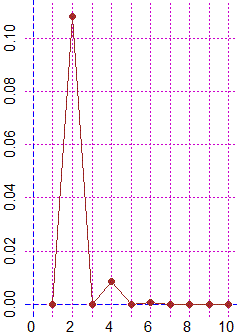
source("http://macosa.dima.unige.it/r.R") A = function(n) ((-1)^n*n+n)*exp(-n)/(n^2+1) D = A(1); for(i in 2:100) D = c(D,A(i)) range(D) # 0.0000000 0.1082682 BF=3; HF=4 Plane(0,10, 0,0.11) polyl(1:10, A(1:10), "brown") POINT(1:10, A(1:10), "brown") A(1:10) # 0.000000e+00 1.082682e-01 0.000000e+00 8.619124e-03 # 0.000000e+00 8.039196e-04 0.000000e+00 8.257542e-05 # 0.000000e+00 8.990085e-06