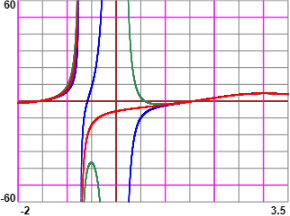
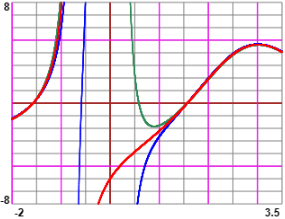
blu: k = 2, verde: k = -2, rosso; k = 0
| Sia f(x) = | x3cos(x) + k cos(x) |
| ———————— | |
| (cos(x)+x) (sin(x)−x) |
(A) Calcolare, al variare di k, il limite di f(x) per x → 0.
(B) Trovare sperimentalmente, nel caso k = 0, l'intervallo
f(I) dove I =
(A) Per x → 0+ cos(x) → 1,
sin(x)−x → 0−; quindi
Per x → 0− sin(x)−x → 0+; quindi
Se k = 0 il limite è quello di
Posso controllare/confermare graficamente. Sotto due grafici realizzati con questo e questo script:


(B). Sicuramente f(I) è un intervallo chiuso e limitato (vedi propr. delle funz. continue e derivabili neGli Oggetti Matematici). Questa parte può essere svolta tutta al computer, con questo script e questo script:
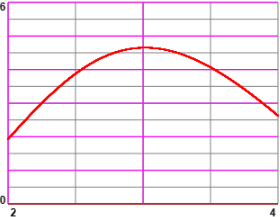
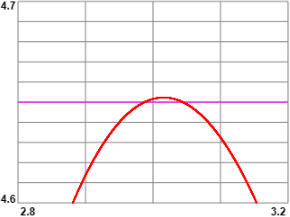
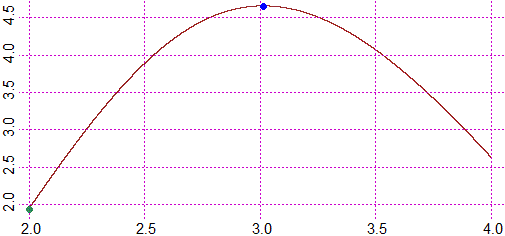
Dal primo grafico deduco che il minimo di f(I) è

e poi arrotondare a 1.93. Dal secondo grafico ricavo che il massimo di f(I) è 4.65. Con WolframAlpha potrei trovarlo facilmente con più esattezza:
Grafici e calcoli fatti con R (vedi).
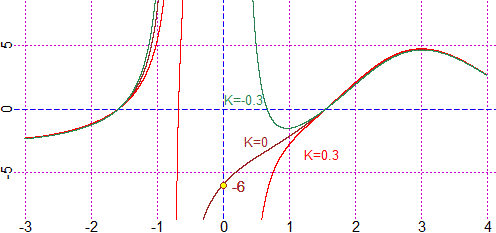
cambio scala: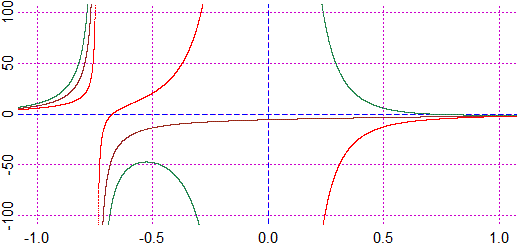
source("http://macosa.dima.unige.it/r.R")
BF=6; HF=3
Plane(-3,4, -8,8)
f = function(x) (x^3+K)*cos(x)/((cos(x)+x)*(sin(x)-x))
K = 0; graph1(f,-3,4, "brown")
K = 0.3; graph1(f,-3,4,"red")
K = -0.3; graph1(f,-3,4,"seagreen")
text(0.5,-2.5,"K=0",cex=0.8,col="brown")
text(1.5,-3.5,"K=0.3",cex=0.8,col="red")
text(0.33,0.8,"K=-0.3",cex=0.8,col="seagreen")
pointO(0,-6, "brown"); text(0.25,-6,"-6",cex=0.9,col="brown")
#
Plane(-1,1, -100,100)
K = 0; graph1(f,-3,4, "brown")
K = 0.3; graph1(f,-3,4,"red")
K = -0.3; graph1(f,-3,4,"seagreen")
# Da grafico e calcoli posso dedurre che se K=0 per x -> 0 f(x) -> -6
K=0; for(N in 1:5) cat(10^-N, '\t', f(10^-N), '\n')
# 0.1 -5.454784
# 0.01 -5.940621
# 0.001 -5.994006
# 1e-04 -5.9994
# 1e-05 -5.999918
# Per K>0 o K<0 il limite da destra e da sinistra sono infiniti opposti
K=0.3; for(N in 2:4) cat(10^-N, '\t', f(10^-N), '\n')
# 0.01 -1782192
# 0.001 -1798201893
# 1e-04 -1.79982e+12
K=0.3; for(N in 2:4) cat(-10^-N, '\t', f(-10^-N), '\n')
# -0.01 1818186
# -0.001 1801801887
# -1e-04 1.80018e+12
K=-0.3; for(N in 2:4) cat(10^-N, '\t', f(10^-N), '\n')
# 0.01 1782180
# 0.001 1798201881
# 1e-04 1.79982e+12
K=-0.3; for(N in 2:4) cat(-10^-N, '\t', f(-10^-N), '\n')
# -0.01 -1818198
# -0.001 -1801801899
# -1e-04 -1.80018e+12
K=0; graph1F(f, 2,4, "brown") x = maxmin(F, 2,4); c( x,f(x) ); more(c( x,f(x) )) # 3.015674 4.652295 # 3.01567396687378 4.65229469036464 POINT(x,f(x), "blue"); POINT(2,f(2), "seagreen"); more(f(2)) # 1.92714916196199