Tracciare, approssimativamente, il grafico e studiare la derivabilità della funzione F così definita:
F(0) = 0, F(x) = sin(1/x) x²

F (posto F(0) = 0, F(x) = sin(1/x) x² per x ≠ 0) è definita in R. Dato che la funzione sin ha valori in [-1,1], abbiamo:
   -1 ≤ sin(1/x) ≤ 1    Essendo x² ≥ 0 ho anche:
   -x² ≤ sin(1/x) x² ≤ x² per ogni x ≠ 0.
F(0) = 0 = 0², quindi:
   -x² ≤ F(x) ≤ x² per ogni x.
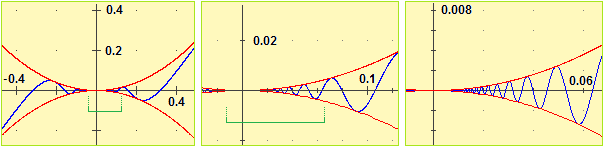
Il grafico di F è quindi costretto tra y = x² e y = −x².
Ne segue che F(x) → 0 per x → 0 (F(x) è compreso tra -x² e x² che tendono a 0).
Dunque F è continua anche in 0, e quindi in tutto R.
Per x → 0+ sin(1/x) oscilla con frequenza crescente. Per x → ∞ 1/x → 0, per cui sin(1/x) ≈ 1/x e, dunque; sin(1/x)x² ≈ x → ∞. L'ultima volta (per x → ∞) che il grafico di F taglia l'asse x, ossia l'ultima volta che sin(1/x) = 0 accade per 1/x = π, ossia per x = 1/π = 0.32 (arrotondando).
Inoltre F ha grafico simmetrico rispetto all'origine in quanto F(-x) = -F(x).
Possiamo concludere che il grafico di F è quello schizzato sotto a sinistra. Si noti che i punti in cui il grafico di F tocca y = x² e y = −x² non sono punti di massimo o minimo relativi in quanto ivi la retta tangente non è orizzontale.

Per quanto riguarda la derivabilità, sappiamo che F è derivabile in R-{0} in quanto ivi lo sono le due funzioni di cui è il prodotto, e che D_x(F(x)) = 2x·sin(1/x) + cos(1/x)·(−1/x²)·x² = 2x·sin(1/x) − cos(1/x). Per x che tende a 0 sia da destra che da sinistra non esiste il limite di D_x(F(x)) in quanto 2x·sin(1/x) tende a 0 mentre cos(1/x) non ha limite.
Ciononstante D_x=0(F(x)) esiste: si vede dal grafico che l'asse x è la retta tangente nell'origine al grafico di F:
la retta che passa per l'origine e per un punto del grafico di F man mano che questo punto si avvina all'origine tende a diventare l'asse x.
Dunque D_x=0(F(x)) = 0. Le figure soprastanti a destra, ottenute zommando il grafico a sinistra, illustrano meglio che cosa accade avvicinandosi all'origine.
Per verificare simbolicamente la cosa facciamo il limite del rapporto incrementale:
lim _h→0 ( F(0+h) - F(0) ) / h = lim _h→0 ( h²sin(1/h) - 0 ) / h = lim _h→0 h sin(1/h) = 0

Questo esempio mette in luce che se una funzione F è continua in un intervallo e sappiamo che è derivabile in esso ma non se lo sia in un punto interno k, se il limite della derivata in x per x che tende a k non esiste non possiamo concludere che la derivata in k non esista (se esiste, nell'ipotesi in cui F sia continua in k, possiamo invece che concludere che la derivata in k esiste e coincide con tale limite).

A destra il grafico fatto con questo semplice script online.     Come si potrebbe realizzare con R (vedi):
source("http://macosa.dima.unige.it/r.R") F = function(x) ifelse(x==0, 0, sin(1/x)*x^2) BF=3.5; HF=2; graph1F(F, -0.1,0.1, "brown") H = function(x) x^2; K = function(x) -x^2 graph1(H,-0.1,0.1,"red") graph1(K,-0.1,0.1,"red")
Vedi anche qui.