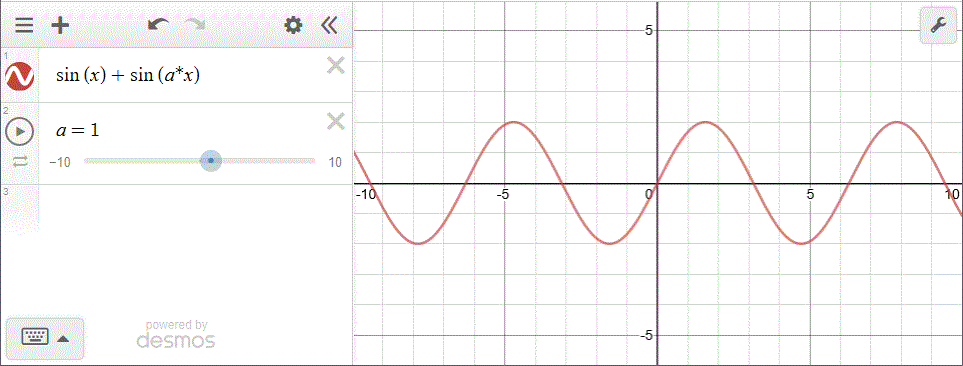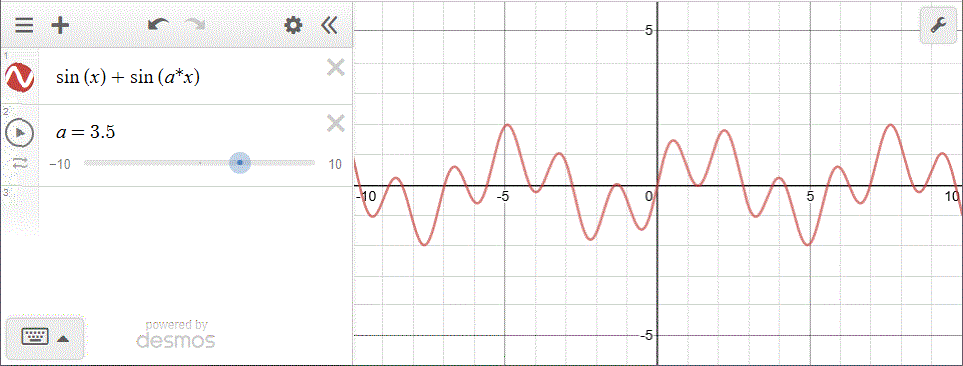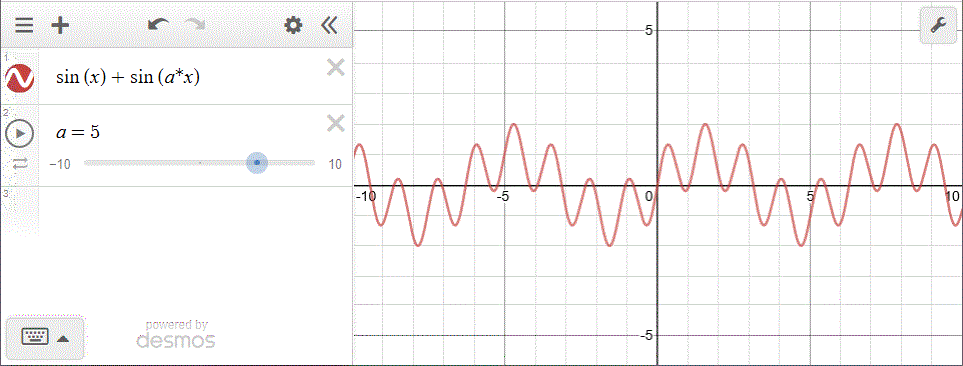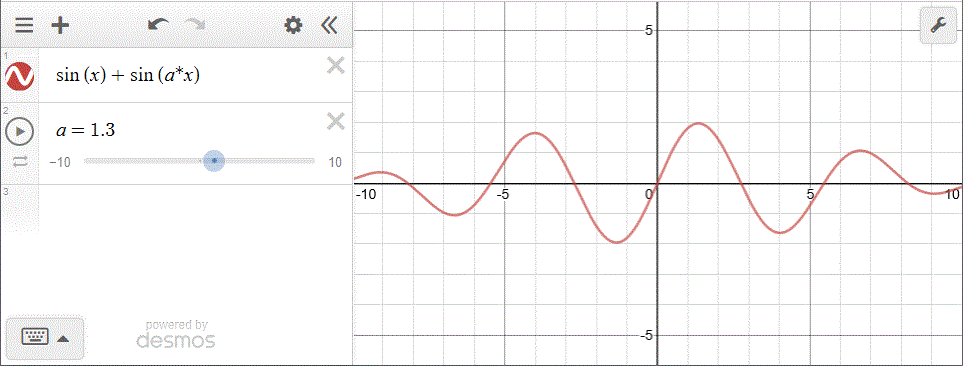
Siano F e G due funzioni periodiche a 1 input e 1 output reali con periodi, rispettivamente, M e N. Con funzione "periodica" qui intendiamo ogni funzione f per cui esiste almeno un numero T diverso da 0 per cui f(x+T) = f(x) per ogni x appartenente al dominio di f. Sia H la funzione x → F(x)+G(x). Quale delle seguenti affermazioni è vera?
(A) H è periodica se F(x) è diverso da k·G(x) per ogni numero reale k
(B) H è periodica se e solo se esiste un numero reale k tale che M = k·N
(C) H è periodica se esiste un numero razionale k tale che M = k·N, ma non in ogni caso in cui esista un numero reale k tale che M = k·N
(D) H è periodica se e solo se se esiste un numero naturale k tale che M = k·N o N = k·M
(E) H è periodica in ogni caso

(B) ed (E) sono equivalenti (a parte il caso in cui uno solo dei due periodi sia nullo); questo fa supporre che nessuna delle due sia la risposta OK.
(A) è evidentemente falsa: sin(x)+sin(x) è periodica.
(D) è falsa.
A destra è illustrato il caso:
F(x) = sin(2x), M = π
G(x) = sin(3x), N = 2/3π
In 3 periodi G percorre 2π, ossia 2 periodi di F.
Quindi F+G (grafico in alto) ogni 3 periodi di G (ossia ogni 2π) si ripete periodicamente.
Qui trovi i grafici realizzati con uno script online.
Qui trovi i grafici realizzati col software online WolframAlpha (vedi).

(B) è falsa.
A destra è illustrato il caso:
F(x) = sin(x), M = 2π
G(x) = sin(√2 x), N = 2π/√2
Il grafico di F+G è ancora simmetrico rispetto a (0,0).
Ma le parti a destra e a sinistra dell'asse y non sono eguali.
Qui trovi i grafici realizzati con uno script online.
Qui trovi i grafici realizzati con WolframAlpha.
Vedi qui se vuoi realizzare i grafici precedenti con R.
Avrei la risposta anche da WolframAlpha battendo:
what is the period of sin(x)+sin(sqrt(2)*x)?

La risposta è (C). Ecco la dimostrazione che il fenomeno vale in generale se M e N hanno rapporto razionale k:
a e b interi, M/N=k=a/b → bM=aN → (F+G)(x+bM)=F(x+bM)+G(x+aN)=F(x)+G(x)

Si può dimostrare (ma la cosa non è banale) che se F e G sono continue vale anche il "solo se". Si possono definire delle funzioni periodiche non continue con periodi incommensurabili la cui funzione somma è periodica.

In un test sottoposto (nel 1999) a una trentina di laureati in matematica, fisica e ingegneria solo il 12% ha risposto correttamente. Il 32% ha scelto E, il 24% D, il 16% B. Il 16% ha preferito non rispondere. In vero, non c'è motivo "razionale" per supporre che F+G sia periodica; è l'abitudine a considerare situazioni in cui i periodi hanno rapporti razionali - o, in genere, interi - a far pensare come "naturale" ciò.

Per un altro semplice esempio che illustri la falsità di (B) si pensi alla somma delle funzioni F e G descritte sotto, F con periodo 1, G con periodo √2:

source("http://macosa.dima.unige.it/r.R")
BF=5; HF=2.5; PLANE(-5,5, -1.5,3.5)
F = function(x) x-floor(x); graph(F, -5,5, "blue")
G = function(x) F(x/sqrt(2))-1; graph(G, -5,5, "red")
# Innalzo di due il grafico della somma per vederlo meglio
H = function(x) G(x)+F(x)+2; graph(H, -5,5, "brown")

Qui trovi i grafici realizzati con WolframAlpha.

Ecco come visualizzare dimanicamente la questione con Cinderella: clicca qui.

e con R: clicca qui.

Con Desmos:

Siano F e G due funzioni periodiche a 1 input e 1 output reali con periodi, rispettivamente, M e N. Con funzione "periodica" qui intendiamo ogni funzione f per cui esiste almeno un numero T diverso da 0 per cui f(x+T) = f(x) per ogni x appartenente al dominio di f. Sia H la funzione x → F(x)+G(x). Quale delle seguenti affermazioni è vera?
	(A) H è periodica se F(x) è diverso da k·G(x) per ogni numero reale k
	(B) H è periodica se e solo se esiste un numero reale k tale che M = k·N
	(C) H è periodica se esiste un numero razionale k tale che M = k·N, ma non in ogni caso in cui esista un numero reale k tale che M = k·N
	(D) H è periodica se e solo se se esiste un numero naturale k tale che M = k·N o N = k·M
	(E) H è periodica in ogni caso