Stabilisci quante soluzioni ha
l'equazione in x
Vi sono diversi modi per rispondere alla domanda. Vediamone alcuni.
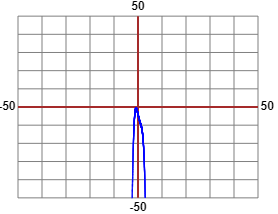
• Il modo più semplice è "ragionare" sul grafico, utilizzando il computer. Impiegando un qualunque programma, ad esempio questo script, tenendo conto che la funzione corrispondente va a -∞ sia "a destra" (per x → ∞) che "a sinistra" (per x → -∞), ottengo:


All'esterno di [-50,50] non può cambiare andamento, essendo di grado 4; infatti le funzioni polinomiali di grado 4 al massimo hanno 3 gobbe (e 2 punti di flesso):

Quindi la nostra equazione non ha soluzioni.
• Disponendo di software per risolvere le equazioni polinomiali di 4° grado, come questo script, posso confermare la risposta:
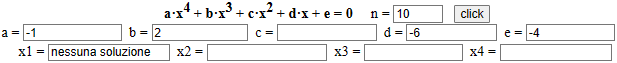
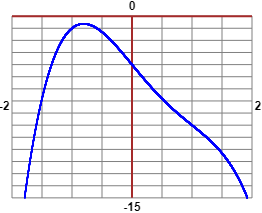
• Vediamo un altro modo in cui procedere senza computer. Un'equazione polinomiale, dopo averla eventualmente trasformata con qualche manipolazione algebrica (ad es. 4x³−2x²+8x=0 la posso trasformare in 2x(2x²−x+8)=0 e, quindi, posso ricondurmi allo studio di x=0 e di 2x²−x+8=0), in alcuni casi molto semplici la posso risolvere facilmente con delle tecniche algebriche. Ma non è questo il caso. Però osservo che derivando due volte la nostra equazione ne ottengo una di 2° grado, che so risolvere. Ecco come potrei procedere se non avessi la possibilità di impiegare il computer.
f(x) = -x^4 + 2*x^3 - 6*x - 4 f'(x) = -4*x^3 + 6*x^2 - 6 = -2*x^2*(2*x - 3) - 6 f"(x) = -12*x^2 + 12*x = -12*x*(x - 1) Il grafico di f ha duunque due flessi, per x=0 e per x=1. In tali punti f vale, rispettivamente, -4 e -9. Quindi il grafico di f ha l'andamento della curva nera sottostante.Non so se passa o tocca l'asse x (le soluzioni sarebbero 2 o 1). o se ne sta al di sotto (nella figura è già tracciato il grafico giusto, assieme a quello di f' e di f"). Calcolo f in -3, -2, -1, 0; ottengo -121, -24, -1, -4. Il massimo realtivo sta tra -2 e 0. In -2, -1, -1/2, 0 ottengo -24, -1, -1.3125, -4. Sta tra -1 e -1/2. (sotto è tracciato il grafico; senza computer posso solo tracciare i punti)
In -0.8 e -0.6 ottengo -0.6336 e -0.9616.
O tra -1 e -0.8 la funzione cresce o tra -0.8 e -0.6 essa decresce.
Il salto massimo è inferiore a 0.4. Essendo la concavità costante (verso il basso) in intervalli più piccoli il salto è minore. Quindi f non arriva al valore 0. Dunque f(x)=0 non ha soluzioni.
• Altrimenti, senza tracciare il grafico, posso usare del software per testare l'equazione. Ad esempio usando questo script, usando il tasto [test]:

posso concludere facilmente che la funzione ha solo valori negativi.
• Potrei anche impiegare WolframAlpha:
solve -x^4 + 2*x^3 - 6*x - 4=0 for x real (no real solutions)