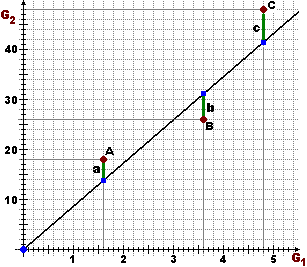
Due grandezze, le cui misure in opportune unità di misura indico con G1 e G2, sono legate da una relazione del tipo G2 = k G1. Voglio determinare k, che so essere una costante positiva.
In tre esperimenti ottengo le coppie (G1,G2) rappresentate a lato con i punti A, B e C. Sono misure effettuate con apparati misuratori ad alta sensibilità, per cui non conosco la precisione delle misure. Per determinare k decido di cercare, tra tutti i grafici del tipo G2 = k G1 (rette passanti per l'origine) come quello raffigurato a fianco, il grafico che rende minima la somma dei quadrati degli scarti tra i valori di G2 sperimentali e quelli che sarebbero stati associati ai valori G1 dalla relazione G2 = k G1. Ossia cerco la pendenza che deve avere una retta passante per l'origine affinché la somma dei quadrati di a, b e c (vedi fig. a lato) sia minima.
(1) Trova il valore di k seguendo questa idea, e approssimalo a due cifre significative. Controlla la soluzione tracciando la retta di cui hai così trovato la pendenza.
(2) Come sopra, cercando la retta per cui è minima |a| + |b| + |c| invece di a²+b²+c².

(1) Sia F(k) = a² + b² + c² = (1.6k-18)²+(3.6k-26)²+(4.8k-48)².
Ho scritto le differenze tutte nella forma pk-q in quanto (q-pk)²=(pk-q)².

F ha per grafico una parabola con la concavità rivolta verso l'alto. Per trovare k per cui F(k) è minimo devo risolvere l'equazione F'(k)=0.

F'(k) = 2((1.6k-18)1.6+(3.6k-26)3.6+(4.8k-48)4.8) = 0 equivale a
k(1.6·1.6+3.6·3.6+4.8·4.8) = 18·1.6+26·3.6+48·4.8 ossia a
k = 352.8/38.56 = 9.14… = 9.1.
Nota. Ho derivato direttamente i termini (pk-q)² senza sviluppare i quadrati: i calcoli sono più semplici.
Capito il procedimento, posso scaricare i calcoli su del software online. Vedi sotto.

La retta corrispondente a questo k a destra è tracciata in rosso. Nel nostro caso, lascia B da una parte e A e C dall'altra.

(2) Con questo secondo metodo, invece della funzione F precedente, di cui a sinistra in alto è tracciato il grafico, considero la funzione:
H(k) = |a| + |b| + |c| = |1.6k-18| + |3.6k-26| + |4.8k-48|.

Si tratta di una funzione continua in quanto ottenuta componendo e sommando funzioni continue. È derivabile tranne che nei punti che corrispondono ad argomenti della funzione valore assoluto in cui questa non è derivabile, ossia per i valori di k che rendono nulli i termini 1.6k-18, 3.6k-26 e 4.8k-48. Negli intervalli delimitati da questi punti avrà andamento lineare in quanto è tale quello delle funzioni polinomiali di 1° grado e quello della funzione valore assoluto a sinistra e a destra di 0. In breve, H è una funzione continua lineare a tratti.
Per k → ∞ e per k → -∞ H(k) → ∞. Quindi il minimo lo si ha in quello tra detti punti in cui H assume il valore minimo. Per k = 18/1.6 = 90/8 ottengo H(k) = 41/2 = 20.5. Per k = 26/3.6 = 65/9 ottengo H(k) = 19.777…. Per k = 48/4.8 = 10 H(k)=12. Dunque per k=10 H(k) assume il valore minimo.
A sinistra è tracciato il grafico di H. Con questo metodo, dunque, avrei preso G2 = 10 G1 invece di G2 = 9.2 G1.
Potrei usare anche, facilmente, WolframAlpha (vedi): minimize |1.6k-18| + |3.6k-26| + |4.8k-48| min = 12 at k = 10

La retta corrispondente a questo k sopra a destra è tracciata in grigio. Passa per il punto C, che corrisponde al punto del grafico di H in cui H assume valore minimo.
Nota. Se H avesse assunto valore minimo in due dei tre valori di k, il grafico di H tra questi due valori sarebbe stato orizzontale, e per tutti i k compresi tra essi avremmo avuto punti di minimo.

Il primo procedimento, per trovare la cosiddetta "retta di regressione", può essere eseguito automaticamente utilizzando lo script online "lin. regression" recuperabile qui:

Posso approssimare la "retta di regressione" con l'equazione y = 9.15 x.

Vedi QUI per il grafico tracciato con un altro script online.

Potevo anche scaricare i calcoli su R (vedi):

source("http://macosa.dima.unige.it/r.R")
x=c(1.6,3.6,4.8); y=c(18, 26, 48); regression(x,y, 0,0)
# 9.149 * x

Due grandezze, le cui misure in opportune unità di misura indico con G1 e G2, sono legate da una relazione del tipo G2 = k G1. Voglio determinare k, che so essere una costante positiva.
In tre esperimenti ottengo le coppie (G1,G2) rappresentate a lato con i punti A, B e C. Sono misure effettuate con apparati misuratori ad alta sensibilità, per cui non conosco la precisione delle misure. Per determinare k decido di cercare, tra tutti i grafici del tipo G2 = k G1 (rette passanti per l'origine) come quello raffigurato a fianco, il grafico che rende minima la somma dei quadrati degli scarti tra i valori di G2 sperimentali e quelli che sarebbero stati associati ai valori G1 dalla relazione G2 = k G1. Ossia cerco la pendenza che deve avere una retta passante per l'origine affinché la somma dei quadrati di a, b e c (vedi fig. a lato) sia minima.
(1) Trova il valore di k seguendo questa idea, e approssimalo a due cifre significative. Controlla la soluzione tracciando la retta di cui hai così trovato la pendenza. (2) Come sopra, cercando la retta per cui è minima \|a\| + \|b\| + \|c\| invece di a²+b²+c².