(1) Trovare una funzione F a input e output in R e un intervallo I di R, il più ampio possibile, tali che F sia derivabile in I, –1 ∈ I, F(–1) = 1 e F'(x) = 1/x.
(2) Sia G la funzione derivata di F. Determinare l'area della figura compresa tra il grafico di G e le rette y = 0, x = –1 e x = –2.

(1)  d log(x) / dx = 1/x, ma x → log(x) non è definita per x=−1. Ma abbiamo anche d log(−x) / dx = 1/x. Hanno la stessa derivata, e sono definte in (−∞,0), tutte le funzioni ottenute aggiungendo una qualunque costante: d (log(−x)+k) / dx = 1/x. [ L'insieme dei termini F(x) tali che F'(x) = 1/x spesso viene indicato in questo modo: F(x) = log(|x|) + k  o, più correttamente: F(x) = log(x) + k1 se x>0, F(x) = log(−x) + k2 se x<0 (k1 e k2 possono essere diversi). 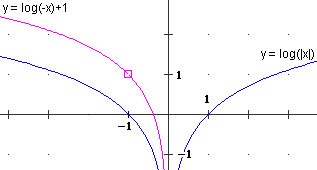Nel nostro caso siamo interessati solo alle funzioni definite in un intervallo, mentre il termine log(|x|) è definito in un intervallo "bucato" in 0; dobbiamo restringerci a (−∞,0), in cui log(|x|) coincide con log(−x) ] Tra le F: x → log(−x)+k quella che vale 1 per x=−1 è F(x) = log(−x)+1 (infatti log(1) = 0: occorre alzare di 1 il grafico di x → log(−x)).

(2)  G(x) = F'(x). Dobbiamo calcolare: | ∫[−2,−1] G | = | F(−1)−F(−2) | = | log(1)−log(2) | = log(2) (= 0.69314718…).

Controllo dell'esercizio con R.

Il campo direzionale, e la curva soluzione, ottenuti con i comandi  diredif  e  soledif:

L'area richiesta, calcolata mediante integrazione (comando  integral), e tracciata col comando  diseq2:

source("http://macosa.dima.unige.it/r.R")
Dy <- function(x,y) 1/x
BF=4; HF=3; Plane(-5,3, -2,3)
diredif(-5,3, -2,3, 25,20)
soledif(-1,1,0,1e4,"blue"); soledif(-1,1,-5,1e4,"blue")
#
G = function(x) 1/x; abs( integral(G, -2,-1) )
#  0.6931472
Plane(-2.5,0.5, -2,1/2)
graph(G, -3,1, "brown")
line(-2,-10,-2,10, "red");  line(-1,-10,-1,10, "red")
P = function(x,y) -2 <= x & x <= -1 & 1/x <= y & y <= 0
diseq2(P,0, "red")   # coloro di rosso dove P > 0, ossia dove è vera