Si può dimostrare che le equazioni polinomiali in x e y di 2° grado rappresentano ellissi, parabole, iperboli, coppie di rette, singole rette, singoli punti o l'insieme vuoto. Stabilisci che tipo di curve sono rappresentate dalle seguenti equazioni studiando il comportamento della pendenza in un punto (x,y) di esse per x che tende a ∞ (o a -∞):
  (A)   x2 + 4y2 − 4xy = y     (B)   x2 − y2 + xy + x − 1 = 0
  (C)   x2 + 2y2 − xy + x + y − 1 = 0

Verifica quanto trovato tracciando i grafici con l'aiuto del computer.

Idea. Lungo una retta y = px+h, indipendentemente da h, il rapporto y/x, ossia (px+h)/x, per x → ∞ tende a p, ossia alla pendenza della retta. Accade lo stesso nel caso di una curva che, per x → ∞, abbia y=px+h come asintoto o la cui derivata prima tenda a p (infatti per il teorema dell'Hopital abbiamo che y/x si comporta come y'/1 = y').
Nota. Esistono anche metodi puramente algebrici, ma forse meno intuitivi e più complessi, per affrontare i problemi proposti.

(A)   x2 + 4y2 − 4xy = y.   Divido per x2:
1 + 4(y/x)2 − 4y/x = y/x2.   Faccio tendere x a ∞ o a -∞ (e variare di conseguenza la corrispondente ordinata y, in modo da stare sulla curva); suppongo che y/x tenda a p; y/x2 tende a 0, e ottengo:
1 - 4p + 4p2 = 0, ossia (1-2p)2 = 0, da cui p = 1/2.
Questa è la pendenza che tende ad assumere la curva.

Questo deve accadere solo per x → ∞ o per x → -∞: si è trovato un unico p, quindi esso deve rappresentare la pendenza dell'asse di simmetria di una parabola (nel caso di una iperbole avremmo trovato due soluzioni distinte). In questo caso è evidente che per x → -∞ l'equazione non è definita (il primo membro è il quadrato di x-2y, per cui y non può tendere, e con lei x, a -∞).

[ Troviamo vertice ed asse di simmetria. Idea: l'asse di simmetria, che ha pendenza 1/2, deve essere perpendicolare nel vertice alla retta tangente. Troviamo la pendenza della tangente nel punto (x,y) derivando l'equazione lasciandola in forma implicita, ossia senza esplicitare y in funzione di x:
dx2/dx + 4 dy2/dx − 4 d(xy)/dx = dy/dx
2x + 4(2y dy/dx) − 4(y dx/dx + x dy/dx) = dy/dx
2x + 8y dy/dx − 4y − 4x dy/dx = dy/dx   ovvero:
y'(8y − 4x -1) = 4y − 2x
y' = (4y − 2x)/(8y − 4x − 1)   Perché la tangente sia perpendicolare all'asse deve essere y' = −1/(1/2) = −2:
-2(8y − 4x -1) = 4y − 2x
È l'equazione che deve soddisfare un punto (x,y) della curva per avere tangente perpendicolare all'asse, ossia per essere il vertice. È l'equazione di una retta.
Intersecando questa retta e la curva trovo il vertice. Riscrivo l'eq. di questa retta:
10y + 5x + 1 = 0. Ma questa retta ha pendenza 2, come l'asse, e, dovendo inetrescare la curva nel vertice, non è altro che l'asse stesso.
A questo punto trovare il vertice è un puro calcolo algebrico. Si ottiene (-3/25, 1/25). ]

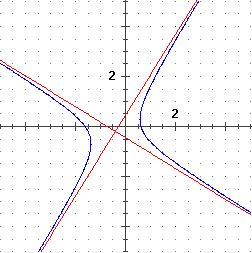
(B)   x2 - y2+ xy + x - 1 = 0.   Divido per x2, faccio tendere x a ∞ o a -∞; suppongo che y/x tenda a p; ottengo:
1 - p2 + p = 0, ossia p2 - p - 1 = 0 che ha soluzioni 1/2 ± √5/2; trovo due valori: devono essere le pendenze dei due asintoti di una iperbole.
[ Per trovare il centro di simmetria dell'iperbole (ossia il punto in cui si intersecano gli asintoti) posso, ad esempio, procedere così:
affinché (x, y) sia centro di simmetria occore che se x2-y2+xy+x-1 si azzera per x = x+h e y = y+k si azzeri anche per x = x-h e y = y-k.
Questo sicuramente accade se impongo che assuma gli stessi valori per x = x±h, ossia, sviluppando i calcoli, che -4x-2y-2 = 0, e che assuma gli stessi valori per y = y±k, ossia che 4y-2x = 0.
Dalle due equazioni ottengo (x, y) = (-2/5, -1/5).
Gli asintoti sono dunque y = (1/2 + √5/2)(x + 2/5) − 1/5 e y = (1/2 − √5/2)(x + 2/5) − 1/5. ]

   (C)   x2 + 2y2 − xy + x + y − 1 = 0.   Dividendo per x2 ottengo 1 + 2(y/x)2 − y/x + 1/x + y/x2 − 1/x2 = 0; se y/x per x → ∞ tendesse a p avremmo al limite 1 + 2p2 − p = 0; questa equazione non ha soluzioni (1+2p2−p = 2(p-1/4)2+7/8).
Ciò corrisponde al fatto che si tratta di una ellisse.
[ Possiamo trovarne il centro di simmetria (x, y) in modo analogo a come si è proceduto sopra, per l'iperbole; otteniamo 4x-2y+2=0, 8y-2x+2=0, da cui (x, y) = (-5/7, -3/7). ]
Un po' più complessa è la determinazione degli assi di simmetria.
Per semplificare i calcoli mi conviene traslare di (-5/7,-3/7) l'ellisse in modo da centrarla nell'origine:  (x-5/7)2 + 2(y-3/7)2 − (x-5/7)(y-3/7) + (x-5/7) + (y-3/7) − 1 = 0 da cui:  x2 + 2y2 − xy − 11/7 = 0

Posso cercare le rette per il centro, ora diventato (0,0), che sono perperdicolari alla curva.
Derivando (implicitamente) rispetto a x l'equazione della curva, pensando y come y(x), come fatto in (A), ottengo:
2x + 4y·y' − (y+xy') − 0 = 0, ossia y'·(4y-x) = -2x+y, ossia y' = (-2x+y)/(4y-x). Questa è la pendenza in un punto (x,y) della curva.
La retta che passa per un punto (x,y) e per O ha pendenza y/x.
La retta è perpendicolare alla curva se (-2x+y)y+(4y-x)x = 0, ossia 2xy+y2-x2 = 0
Cerco p = y/x. Divido per x2, ottenendo: 2x/y+(y/x)2-1 = 0, ossia: 2p+p2-1 = 0.
Risolvendo questa equazione trovo che le pendenze dei due assi sono -1-√2 e -1+√2. Dato che atan(-1+√2) = 22.5°, l'asse maggiore è ruotato di 22.5° rispetto all'asse y.

Quanto visto può essere generalizzato:
una eq. polinomiale di 2° grado  Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 (con A, B e C non tutti nulli) dividendo per x2 e ipotizzando che y/x → p al tendere a ∞ o -∞ di x, dà luogo alla equazione  A + Bp + Cp2 = 0,  che equivale a
(p + B/(2C))2 = B2 − 4AC,  se C ≠ 0, o a p = −B/(2C) ± √(B2 − 4AC), se inoltre B2−4AC ≥ 0.
• Se l'equazione ha due soluzioni reali (B2−4AC>0) siamo di fronte a un'iperbole, o al caso limite di una coppia di rette che si intersecano (es.: x2−y2=0 o xy=0).
• Se l'equazione non ha soluzioni reali (B2−4AC<0) siamo di fronte a un'ellisse, o al caso limite di un punto (es.: x2+y2=0) o dell'insieme vuoto (es.: x2+y2=−1).
• Se l'equazione ha 1 soluzione reale (B2−4AC=0) siamo di fronte a una parabola, o al caso limite di una retta (es.: x2+2hx+h2=0) o dell'insieme vuoto (es.: x2+2hx+h2=−1).

Ecco come ottenere i grafici con R.