Calcola le prime tre delle seguenti derivate "a mano", controlla i risultati con opportuno software, spiega, infine, il procedimento che hai impiegato. Calcola la quarta derivata utilizzando opportuno software, spiegando come hai proceduto.

d (5*x^2+3*x)*(6*x^2-4) / dx      d 3*x^2/(4*x^2+5) / dx      d (3*x^2-5*x+1)^3 / dx
F'(9) dove F è la funzione inversa di G: x → x^7-x^2+x-3.

    Prime tre derivate.

d (5*x^2+3*x)*(6*x^2-4) / dx = (5*2*x+3)*(6*x^2-4)+(5*x^2+3*x)*6*2*x = 2*5*2*6*x^3 + 3*3*6*x^2 - 4*5*2*x - 12 = 2*(60*x^3+27*x^2-20*x-6)

d 3*x^2/(4*x^2+5) / dx = (3*2*x*(4*x^2+5)-3*x^2*4*2*x)/(4*x^2+5)^2 = (30*x)/(4*x^2+5)^2

d (3*x^2-5*x+1)^3 / dx = 3*( (3*2*x-5) * (3*x^2-5*x+1)^2 ) = 3*(6*x-5)*(3*x^2-5*x+1)^2

Posso controllare i risultati con www.wolframalpha.com. Basta ad es. introdurre d (5*x^2+3*x)*(6*x^2-4) / dx.
Con R (vedi) ottengo quello descritto sopra nel primo passaggio (il calcolo usando le regole di derivazione, senza le successive semplificazioni). Oppure posso sviluppare prima le moltiplicazioni.

source("http://macosa.dima.unige.it/r.R")
h = function(x) (5*x^2+3*x)*(6*x^2-4)
deriv(h,"x")
# (5*(2*x) + 3) * (6*x^2 - 4) + (5*x^2 + 3*x) * (6 *(2*x))
P = c(5,3,0); Q = c(6,0,-4); prodp(P,Q)
# 30  18 -20 -12   0
h1 = function(x) 30*x^4+18*x^3-20*x^2-12*x
deriv(h1,"x")
# 30*(4*x^3) + 18*(3*x^2) - 20 *(2*x) - 12

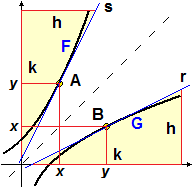
    Calcolo di D(F)(9). La derivata di una funzione F in x (vedi figura sotto a sinistra) è il reciproco delle derivata della funzione inversa G nel punto del suo grafico di ordinata x.  Nel nostro caso x = 9, F'(9) = 1/G'(y) dove y = F(9), ovvero G(y) = 9.  Prima di metterci a fare i calcoli stimiamo graficamente il valore di F'(9), ovvero il valore del reciproco della pendenza di G nel punto di ordinata 9. Ecco sotto, a centro e a destra alcuni grafici. Si ottiene come stima grafica F'(9) ≈ (1.438-1.434)/(G(1.438)-G(1.434)) = 0.0168. Volendo ci si può fermare qui.

G = function(x) x^7-x^2+x-3

Possiamo, volendo, affrontare il problema analiticamente. Risolviamo l'equazione G(y)−9 = 0. Procediamo con R, ma avremmo potuto procedere impiegando un qualunque algoritmo per la ricerca degli zeri di una funzione continua.

BF=3; HF=3
Plane(-20,20, -20,20); graph(G, -20,20, "brown")    # cambio scala
Plane(-2,2, -4,12); graph(G, -2,2, "brown")         # cerco quando G vale 9
p = solution(G,9, 1,1.5); p
# 1.436579
POINT(p,9, "red")
# la derivata di F è il reciproco della derivata di G
dG = function(x) eval(deriv(G,"x"))
D = 1/dG(p); more(D)
# 0.0167630136849024
F1 = function(y,x) G(x)-y
Plane(-4,15, -1,2); CURVE(F1, "brown")
POINT(9,p, "red")
F2 = function(x) D*(x-9)+p; graph1(F2,-4,15, "red")

G                                 G                                         F

Con WolframAlpha si possono, volendo, ottenere più cifre. Posso risolvere con quante cifre voglio l'equazione x^7-x^2+x-3 = 9 col comando  solve x^7-x^2+x-3 = 9 for x  e, poi, posso usare il valore ottenuto per trovare, con la precisione che voglio, F'(9). Ad esempio: 0.016763013684902427733767417745912246583916630484207…

Richiami qui.