
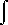
Allora:
| x |  | ||
| Definiamo, per x ∈ [0,6], F(x) = | 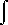 | f | |
| 0 | ||
| dove f ha il grafico a lato. Allora: | |||
| A) 2 è l'unico punto di massimo assoluto di F | D) 6 è punto di massimo locale di F | |
| B) f non è integrabile e quindi F non è ben definita | E) 1 è punto di massimo locale di F | |
| C) 1 è l'unico punto di massimo assoluto di F | ||
| Possiamo ragionare in due modi: interpretare F(x) come l'area tra grafico di f e asse x nella striscia con ascissa compresa tra 0 e x, o interpretare F come antiderivata (primitiva), ossia pensare che F'=f, con la condizione F(0)=0. Il primo modo in questo caso è più facile del secondo: | |
| – l'area cresce per x che va da 0 a 2; – in 2 il grafico interseca l'asse x e poi si aggiunge all'area un contributo negativo, che quando si arriva a x=4 eguaglia in valore assoluto il contributo positivo iniziale, accumulatosi per x tra 0 e 2: F tra 2 e 4 decresce e F(4)=0; – poi tra 4 e 6 il grafico sta sopra l'asse x, aggiungendo all'area un contributo positivo uguale al contributo positivo iniziale, in quanto si tratta di un triangolo di area uguale: F tra 4 e 6 cresce e F(6)=F(2). |  |
| Quindi in 2 e 6 F ha massimi relativi: la risposta OK è D | |
Di fronte a questo quesito, in un test sottoposto a una cinquantina di laureati in matematica, fisica e ingegneria (nel 2001) solo il 30% delle persone ha risposto correttamente, nonostante la facilità del quesito per un laureato del genere. Il 19% ha scelto E, trasferendo a F l'andamento di f. Il 13% ha scelto A, non prendendo in considerazione 6, forse perché all'estremo destro del dominio. Il 23% ha preferito non rispondere. Gli altri sono sono più o meno ripartiti sulle altre due risposte.
I grafici con R (vedi):
source("http://macosa.dima.unige.it/r.R")
f = function(x) ifelse(x < 1,x,ifelse(x < 3,-x+2,ifelse(x < 4,x-4,0.5*(x-4))))
BF=3.5; HF=2.5; graphF( f, 0,6, "black")
Z = function(x) 0; Diseq(f,Z, 0,6, "blue"); Diseq(Z,f, 0,6, "orange")
graph( f, 0,6, "black"); GintegraC(f,0,6,"magenta")
