Data la funzione x → x4 − 2x3 + 7x − 5, studiane
l'andamento, compresa la concavità, eventualmente trovando
alcuni valori (zeri o punti di massimo o minimo o …) in forma approssimata.
Si tratta di una funzione polinomale di grado pari e di coefficiente direttivo
positivo, quindi per l'input che tende a ∞ o a −∞
tende a ∞. Potrebbe avere da 0 a 4 zeri.
Se disponiamo di un computer possiamo facilmente stabilire che
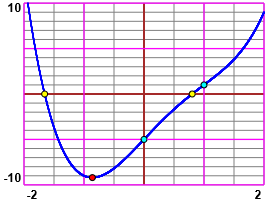
l'andamento è quello rappresentato a fianco. Altrimenti la cosa più
semplice è determinare le sue derivate. Indichiamo con F la funzione:
F '(x) = 4x³−6x²+7,
F "(x) = 12x²−12x
= 12x(x−1). F "(x) = 0
sse x=0 o x=1. F '(0) = 7,
F '(1) = 5;
quindi in 0 e in 1 abbiamo flessi ascendenti.
Le ordinate corrispondenti sono
F(0) = −5,
F(1) = 1. Quindi potremmo schizzare il grafico a fianco.
Volendo trovare con più precisione le coordinate dei punti (gialli) in
cui il grafico taglia l'asse x e in cui raggiunge il punto (rosso) più basso possiamo
procedere per tentativi ragionati, o usare dei programmi per la ricerca degli zeri.
Vediamo come procedere facilmente con degli script online. Usiamo in particolare la
"nostra" calcolatrice (vedi).
|
 |
Iniziamo cercando direttamente il punto di minimo.
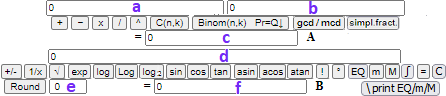
In [d]: pow(Q,4) - 2*pow(Q,3) + 7*Q - 5
In [a] e [b]: -2 2
Clicco ripetutamente [m] (e quando voglio [ \ print ...]):
Q= -0.6666666666666667 dif= 2.6666666666666665 F(Q)= -4.802469135802469
...
Q= -0.8609461519970503 dif= 7.145696934163226e-8 F(Q)= -9.200888440844128
Q= -0.8609461400875554 dif= 4.763797956108817e-8 F(Q)= -9.200888440844137
Q= -0.8609461480272187 dif= 3.175865304072545e-8 F(Q)= -9.200888440844139
Q= -0.8609461533203275 dif= 2.117243536048363e-8 F(Q)= -9.200888440844139
Il punto "rosso" è (-0.86094614, -9.2008884408441)
Potevo anche, in alternativa, e con maggiore precisione, cercare dove si azzera la derivata prima:
In [d]: 4*pow(Q,3) - 6*pow(Q,2) + 7
In [a] e [b]: -2 2
Clicco ripetutamente [EQ] (e quando voglio [ \ print ...]):
...
Q= -0.8609461421185722 dif= 1.7763568394002505e-15 F(Q)= -1.3322676295501878e-14
Q= -0.8609461421185718 dif= 8.881784197001252e-16 F(Q)= -5.329070518200751e-15
Q= -0.8609461421185716 dif= 4.440892098500626e-16 F(Q)= -4.440892098500626e-16
Q= -0.8609461421185715 dif= 2.220446049250313e-16 F(Q)= 1.3322676295501878e-15
Q= -0.8609461421185716 dif= 1.1102230246251565e-16 F(Q)= 2.6645352591003757e-15
Q= -0.8609461421185716 dif= 1.1102230246251565e-16 F(Q)= 4.440892098500626e-16
Il punto di minimo è (-0.86094614211857, -9.2008884408441)
Determiniamo il valore degli zeri. Il primo:
In [d]: pow(Q,4) - 2*pow(Q,3) + 7*Q - 5
In [a] e [b]: -2 -1
Clicco ripetutamente [EQ] (e quando voglio [ \ print ...]):
Q= -1.75 dif= 0.5 F(Q)= -6.34375
...
Q= -1.6556007213929576 dif= 2.842170943040401e-14 F(Q)= -9.237055564881302e-14
Q= -1.6556007213929647 dif= 1.4210854715202004e-14 F(Q)= -2.877698079828406e-13
Q= -1.655600721392961 dif= 7.105427357601002e-15 F(Q)= 5.329070518200751e-15
Q= -1.6556007213929593 dif= 3.552713678800501e-15 F(Q)= -4.440892098500626e-14
Q= -1.6556007213929602 dif= 1.7763568394002505e-15 F(Q)= -6.838973831690964e-14
Il secondo:
In [a] e [b]: 0 1
...
Q= 0.8027663827371374 dif= 4.440892098500626e-16 F(Q)= 2.220446049250313e-15
...
Q= 0.8027663827371372 dif= 1.1102230246251565e-16 F(Q)= -4.440892098500626e-16
Controllando con WolframAlpha (vedi) troveremmo i valori
-1.655600721392960923578812 e 0.8027663827371373905760157.
Il grafico precedente è stato tracciato con questo
script online.
Richiami:  concavità di una funzione neGli Oggetti Matematici.
concavità di una funzione neGli Oggetti Matematici.
Come ottenere grafico ed esiti numerici usando R. F <- function(x) x^4-2*x^3+7*x-5
q = c(-5, 7, 0, -2, 1); solpol(q)
# 0.80276638273714 -1.655600721393 Gli zeri del polinomio
# Senza usare il fatto che è un polinomio
Plane(-2,2, -10,10); graph1(F, -2,2, "brown")
solution(F,0, 0,1); solution(F,0, -2,0)
# 0.8027664 -1.655601
Point(solution(F,0, 0,1),0,"black"); Point(solution(F,0, -2,-1),0,"black")
m = minmax(F,-2,1); m; F(m)
# -0.8609461 -9.200888
Point(m,F(m),"blue")
deriv2(F,"x")
# 4 * (3 * x^2) - 2 * (3 * (2 * x)) 0-12*x+12*x^2
solpol(c(0,-12,12))
# 0 1
Point(0,F(0),"red"); Point(1,F(1),"red")
|


