Dopo aver rivisto questo esercizio (e la sua soluzione), schizza il grafico della funzione x → ∫ _[0,x] sin(u)/u du per x tra −50 e 50 e prova ad individuare, se esistono, i valori di ∫ _[0,∞] sin(u)/u du e di ∫ _[−∞,∞] sin(u)/u du.

Sopra sono tracciati i grafici di x → sin(x)/x e di x → ∫ [1,x] sin(u)/u du a destra dell'origine. Per la simmetria del grafico di x → sin(x)/x rispetto all'asse delle y (tracciato a destra) posso concludere che x → ∫ [0,x] sin(u)/u du ha grafico simmetrico rispetto alla origine, ossia che ha la forma seguente:

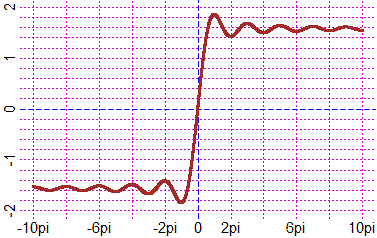
Per tracciarlo posso usare per semplicità il comando Gintegra che traccia il grafico di una funzione intergarle. Lo uso a sinistra e a destra di 0 in modo da evitare il punto in cui l'integranda non è definita:

BF=4.5; HF=3
TICKx=2*pi; TICKy=0.2; Plane2(-10*pi,10*pi,-2,2)
underX(c("-10pi","-6pi","-2pi","0","2pi","6pi","10pi"),2*pi*c(-5,-3,-1,0,1,3,5))
underY(-2:2,-2:2)
g = function(x) sin(x)/x
Gintegra(g,0,10*pi, "brown")
Gintegra(g,0,-10*pi, "brown")

Per quanto visto nell'esercizio citato, ∫ _[0,∞) sin(u)/u du = π/2 e quindi ∫ _(-∞,∞) sin(u)/u du = π. Per approfondimenti vedi qui.

Vediamo anche come si potrebbe usare lo script "integ.", recuperabile qui, prendendo if(x==0) {u=1} else {u=sin(x)/x}; return u come "F(x)"; ottengo:

3.1416126411313816  if a=-100000 b=100000 n=1e7 [-3.301820106216269e-8]
3.1416126741495827  if a=-100000 b=100000 n=1e6 [3.1416126741495827]
 - - - - - - - -
3.1417830908034126  if a=-10000 b=10000 n=1e7 [-3.1422353607979403e-9]
3.141783093945648  if a=-10000 b=10000 n=1e6 [3.141783093945648]
 - - - - - - - -
3.140466243750379  if a=-1000 b=1000 n=1e6 [1.8531459922144222e-8]
3.140466225218919  if a=-1000 b=1000 n=1e5 [3.140466225218919]
 - - - - - - - -
3.124450933749163  if a=-100 b=100 n=1e6 [2.8623210468481375e-9]
3.124450930886842  if a=-100 b=100 n=1e5 [3.124450930886842]

∫ _[-100,100] = 3.124450934, ∫ _[-1000,1000] = 3.14046624, ∫ _{[-10000,10000]} = 3.14178309; è facile congetturare che tra -∞ e ∞ l'integrale sia π.