Determina il volume del solido raffigurato a lato, dotato di un asse di simmetria, con la superficie "interna" cilinidrica di raggio uguale all'altezza, una faccia a forma di corona circolare e il resto della superficie a profilo rettilineo, inclinato di 45° rispetto all'asse di simmetria (i semipiani aventi come bordo l'asse di simmetria intercettano sul solido dei triangoli rettangoli isosceli). L (la lunghezza dei cateti del triangolo T) è sia lo spessore della corona circolare che l'altezza e il raggio del cilindro. Per il calcolo sviluppa un opportuno integrale, supponendo di non sapere come calcolare il volume del cono, con un metodo che funzionerebbe anche se il profilo della superficie esterna non fosse rettilineo.

Controlla il risultato utilizzando la formula per il calcolo del volume del cono.

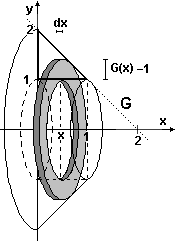Suppongo che L=1, ossia determino il volume usando come unità L³. Conoscendo la formula per il volume del cono posso pensare il solido come un cono (circolare retto) di altezza e raggio 2 da cui ho tolto un cono di altezza e raggio 1 e un cilindro (circolare retto) di altezza e raggio 1: ottengo 4π2/3-π/3-π = 4π/3 (ossia 4π/3L³).
Usando un metodo di integrazione, penso il solido come frutto della rotazione di una figura attorno all'asse di simmetria. Nel mio caso posso pensare il profilo della figura sia come grafico di una funzione F assumendo l'asse di rotazione come asse y che come quello di una funzione G assumendo l'asse di di rotazione come asse x.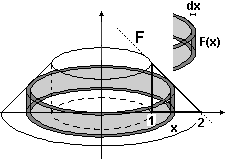

Col secondo metodo (figura a sinistra) penso il solido come somma di tanti anelli (rondelle) di spessore Δx, raggio esterno G(x) e interno 1: la variazione ΔV del volume al passare da x a x+Δx è approssimabile con π(G(x)²-1) (area della corona circolare base dell'anello) per Δx: dV = π(G(x)²-1)dx.
G(x) = 2-x. Dato che x varia in I = [0,1], il volume è V = ∫_Iπ(3+x²)dx = π(3x+x³/3)_x=1 = π(3+1/3) = 4π/3.

Col primo metodo (figura a destra) penso il solido come somma di cilindretti cavi (gusci cilindrici) di spessore Δx, raggio interno x e altezza F(x): la variazione ΔV del volume al passare da x a x+Δx è approssimabile con F(x)Δx (area del rettangolino dalla cui rotazione ottengo il cilindretto cavo) per 2πx (circonferenza del cilindretto): dV = 2πxF(x)dx.
F(x) = 2-x (in questo caso particolare F(x)=G(x)). Dato che x varia in I = [1,2], il volume è V = ∫_I2π(2x-x²)dx = 2π((x²-x³/3)_x=2 - (x²-x³/3)_x=1) = 2π(3-7/3) = 4π/3.

Per commenti, guardare Altri usi degli integrali

Calcoli e disegni col software online WolframAlpha:

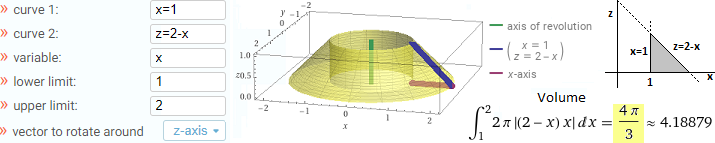
Volendo fare il grafico con R:

par( mai = c(0.2,0.2,0.2,0.2) )
cerchio <- function(r,c1,c2,h,c) {t <- seq(0,2*pi,len=360);
         lines(trans3d(cos(t)*r+c1,sin(t)*r+c2,h,pmat=F),col=c) }
x <- c(-2,2); y <- c(-2,2); z0 <- c(0,1)
u <- rep(z0[1],4); z <- array(u,dim=c(2,2))
th <- 30; ph <- 50
F <- persp(x,y,z,theta=th,phi=ph,scale=FALSE,zlim=z0,xlim=x,ylim=y,d=1)
for(v in seq(0,1,len=15)) cerchio(1,0,0,v,"red")
for(v in seq(0,1,len=20)) cerchio(2-v,0,0,v,"blue")
lines(trans3d(c(0,0),c(0,0),c(0,z0[2]),pmat=F),col="blue",lty=3)
lines(trans3d(c(0,x[2]),c(0,0),c(0,0),pmat=F),col="blue",lty=3)
lines(trans3d(c(0,0),c(0,y[2]),c(0,0),pmat=F),col="blue",lty=3)
# Prova con altri ph tra -90 e 90 (ad es. ph <- 10 ): copia da F in
# poi (e incolla quanto hai copiato)

	Suppongo che L=1, ossia determino il volume usando come unità L³. Conoscendo la formula per il volume del cono posso pensare il solido come un cono (circolare retto) di altezza e raggio 2 da cui ho tolto un cono di altezza e raggio 1 e un cilindro (circolare retto) di altezza e raggio 1: ottengo 4π2/3-π/3-π = 4π/3 (ossia 4π/3L³). Usando un metodo di integrazione, penso il solido come frutto della rotazione di una figura attorno all'asse di simmetria. Nel mio caso posso pensare il profilo della figura sia come grafico di una funzione F assumendo l'asse di rotazione come asse y che come quello di una funzione G assumendo l'asse di di rotazione come asse x.
Col secondo metodo (figura a sinistra) penso il solido come somma di tanti anelli (rondelle) di spessore Δx, raggio esterno G(x) e interno 1: la variazione ΔV del volume al passare da x a x+Δx è approssimabile con π(G(x)²-1) (area della corona circolare base dell'anello) per Δx: dV = π(G(x)²-1)dx. G(x) = 2-x. Dato che x varia in I = [0,1], il volume è V = ∫_Iπ(3+x²)dx = π(3x+x³/3)_x=1 = π(3+1/3) = 4π/3.
Col primo metodo (figura a destra) penso il solido come somma di cilindretti cavi (gusci cilindrici) di spessore Δx, raggio interno x e altezza F(x): la variazione ΔV del volume al passare da x a x+Δx è approssimabile con F(x)Δx (area del rettangolino dalla cui rotazione ottengo il cilindretto cavo) per 2πx (circonferenza del cilindretto): dV = 2πxF(x)dx. F(x) = 2-x (in questo caso particolare F(x)=G(x)). Dato che x varia in I = [1,2], il volume è V = ∫_I2π(2x-x²)dx = 2π((x²-x³/3)_x=2 - (x²-x³/3)_x=1) = 2π(3-7/3) = 4π/3.