La crescita esponenziale
Studiamo un altro fenomeno di crescita esponenziale. Vi sono vari tipi di microrganismi unicellulari che si riproducono per scissione: quando la cellula raggiunge una
certa dimensione si scinde in due. In particolari condizioni ambientali all'interno di una popolazione di una
di queste specie di microrganismi il tempo medio di vita di una cellula (ossia il tempo medio che passa
dalla scissione di una cellula a quello di una cellula da essa generata) è pressocché costante.
In alcuni microrganismi esso può essere di pochi minuti, in altri può essere di qualche giorno.
In queste condizioni esiste un intervallo di tempo T (tempo di duplicazione) tale che,
passando da un qualunque istante t all'istante t+T, la popolazione raddoppi:
infatti gli organismi non si scindono tutti esattamente nello stesso tempo,
cosicché nel complesso di una popolazione di svariati milioni di individui si ha un ininterrotto
duplicarsi di cellule che dà luogo a una crescita della popolazione praticamente continua e regolare, con velocità
di variazione proporzionale alla popolazione stessa.
Se iniziamo a misurare la popolazione a partire da un certo istante t = 0 e indichiamo con P(t) il numero per cui si è moltiplicata
dopo il tempo t,
ossia se P(t) è la popolazione misurata prendendo come unità la popolazione iniziale,
possiamo descrivere la situazione così:
P(0) = 1, P(t+T) = P(t)·2
[1] Se n è il numero delle duplicazioni avvenute nel tempo t, quali tra le seguenti formule esprime P(t)? Perché?
(a) P(t) = 2 + n
(b) P(t) = 2 · n
(c) P(t) = 2t
(d) P(t) = 2n
[2] Tenendo conto che n lo si ottiene dividendo t per il tempo di duplicazione T, abbiamo anche:
(a) P(t) = 2 t / T
(b) P(t) = 2 T / t
(c) P(t) = 2 · T / t
(d) P(t) = 2 + t / T
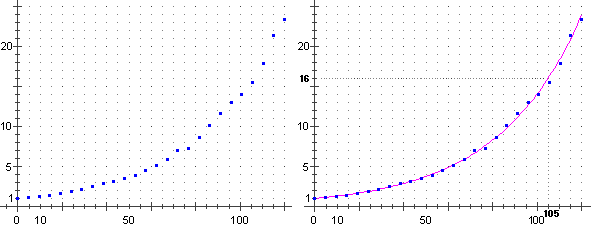
Se da un rilevamento sperimentale ogni 5 minuti otteniamo i valori di P rappresentati graficamente sotto a sinistra, possiamo cercare di approssimare tali punti con una curva, come è fatto sotto a destra.

Ricaviamo che la popolazione si moltiplica per 16 in 105 minuti; 16 = 24; quindi 4T = 105 minuti.
Questi microrganismi duplicano la loro popolazione in 105/4 = 26.25 minuti, ossia in
L'andamento di P in questo caso è dunque descrivibile con P(t) =
2 t / 26.25.
Poiché, con una calcolatrice, ho che 21/26.25 = 1.0268, posso descrivere il fenomeno anche con la formula:
P(t) = 1.0268 t.
[3] Per ottenere la formula precedente si è usata la proprietà: a b · c = (ab )c. Che cosa si sono presi come a, b e c? a = .... b = .... c = ....
Anche questa è una crescita esponenziale. In questo caso l'esponente non varia solo tra
i numeri naturali, come nel caso della catena di Sant'Antonio (in cui valutavamo il tempo di settimana in settimana), ma sui numeri reali (possiamo considerare quanti sono i microrganismi in un
qualunque istante t).
Pure in questo caso la velocità con cui varia P(t) è proporzionale a