Usando il goniometro ho la conferma: tra un lato e l'altro vi sono 90 spicchietti da 1°, ovvero 9 spicchi da 10° (8 spicchi interi da 10° e 2 mezzi spicchi).
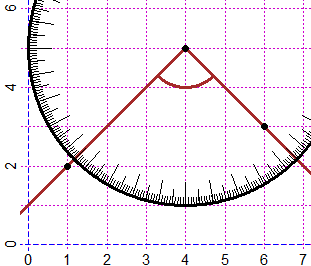
| A fianco è tracciato l'angolo ∠ABC con A=(1,2), B=(4,5), C=(6,3). Utilizzando il goniometro raffigurato, determina quanto esso è ampio. |  |
|
È facile capire che si tratta di un quarto di giro, cioè che l'angolo è retto,
e quindi ampio 90°. Usando il goniometro ho la conferma: tra un lato e l'altro vi sono 90 spicchietti da 1°, ovvero 9 spicchi da 10° (8 spicchi interi da 10° e 2 mezzi spicchi). |
 |
Per l'insegnante. La figura è stata tracciata con R: vedi sotto. A sinistra la figura tracciabile con uno script online: vedi (Px=[1,4,6]; Py=[2,5,3]; L6x=[0,4,9]; L6y=[1,5,0]; gr1=225; gr2=315) source("http://macosa.dima.unige.it/r.R")
PLANE(0,7,0,7)
A1=1;A2=2; B1=4;B2=5; C1=6;C2=3
halfline(B1,B2, A1,A2,"brown")
halfline(B1,B2, C1,C2,"brown")
POINT(c(A1,B1,C1),c(A2,B2,C2),"black")
Gonio(B1,B2, 4)
ARC(4,5, 1, 225,225+90, "brown")
angle(c(A1,A2),c(B1,B2),c(C1,C2))
# 90 ok: l'angolo è di 90°
|
L'insegnante per preparare esercizi come questo può usare script online come questo, che può poi essere fatto usare anche agli alunni.
