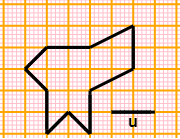
A lato è riprodotta la rappresentazione cartografica su carta millimetrata della base di un castello che ha un'estensione di 1200 m2. Qual è la scala di riduzione della cartina? Ovvero quale è la lunghezza u che rappresenta un segmento lungo 1 cm?

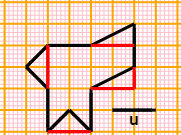
Come evidenzia l'immagine a lato, la figura ha l'estensione di 3 cm2. Quindi 1 cm2 sulla carta rappresenta 1200/3 = 400 m2. Un quadrato di area 400 m2 ha lato di 20 m (400=20). Quindi 1 cm sulla carta rappresenta u = 20 m. 20 m = 20·100 cm = 2000 cm. La figura è quindi 1/2000 della realtà: 1/2000 (ovvero 1:2000 ovvero 0.0005) è la scala di riduzione. Si poteva arrivare alla soluzione anche procedendo così: DistanzaReale/DistanzaSuCarta = √(AreaReale/AreaSuCarta) = √(1200 m2 / 3 cm2) = √(12000000 cm2 / 3 cm2) = √(4000000) = 2000.

Sui fattori di scala e sulla proprietà additiva: diagrammi e area neGli Oggetti Matematici.

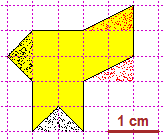
Il docente può realizzare le figure facilmente online con lo script disegnare(4): vedi  (leggi l'help, in cui sono presenti anche queste due figure).

# Come è fattibile la figura con R
                                  
source("http://macosa.dima.unige.it/r.R")
BF=2.5; HF=2.5
GRIGLIAs(0,6,0,6)  # traccio una griglia senza assi
x=c(0,1,1,2,3,3,5,5,3,1,0)
y=c(3,2,0,1,0,2,3,5,4,4,3)
spezzaC(x,y,"yellow")
BOXs()             # ritraccio la griglia senza assi
P = function(x,y) y < -abs(x-2)+1 & y > 0
diseq2(P,0, "black")
P = function(x,y) x > abs(y-3) & x < 1
diseq2(P,0, "black")
P = function(x,y) y < x/2+1/2 & y > 2 & x < 5
diseq2(P,0, "red")
P = function(x,y) y < x/2+5/2 & y > 4 & x < 5
diseq2(P,0, "red")
segm(4,0, 6,0, "brown"); scrivi(5,1/2, "1 cm")
spezza(x,y,"black")         # ritraccio il poligono
##
## ovvero:
BF=2.5; HF=2.5
GRIDw(0,6,0,6)  # traccio una griglia senza assi
x=c(0,1,1,2,3,3,5,5,3,1,0)
y=c(3,2,0,1,0,2,3,5,4,4,3)
polyC(x,y,"yellow")
BOXw()             # ritraccio la griglia senza assi
P = function(x,y) y < -abs(x-2)+1 & y > 0
diseq2(P,0, "black")
P = function(x,y) x > abs(y-3) & x < 1
diseq2(P,0, "black")
P = function(x,y) y < x/2+1/2 & y > 2 & x < 5
diseq2(P,0, "red")
P = function(x,y) y < x/2+5/2 & y > 4 & x < 5
diseq2(P,0, "red")
segm(4,0, 6,0, "brown"); type(5,1/2, "1 cm")
polyl(x,y,"black")         # ritraccio il poligono