Nel triangolo disegnato a fianco il segmento CQ taglia a metà l'angolo di vertice C e il segmento AP taglia a metà l'angolo di vertice A. Puoi concludere qualcosa circa le distanze di R dalle rette su cui stanno i tre lati del triangolo?

Le tre bisettrci dei vertici di un triangolo si incontrano, tutte e tre, in un punto comune.  E questo punto è il centro del cerchio inscritto nel triangolo (vedi). Quindi le distanze di R dai tre lati (le lunghezze dei segmenti rossi nella figura a destra) sono eguali. Il prolungamento della bisettrice dell'angolo in B (che non è stato disegnato) non passa esattamente per il raggio perpendicolare ad AC.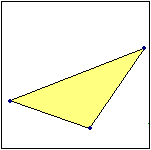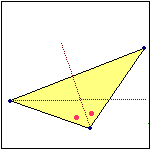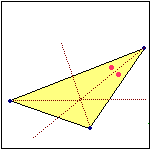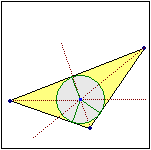

   

# Se l'insegnante vuol fare figure analoghe con R:
source("http://macosa.dima.unige.it/r.R")
BOXW(0,11, 0,10)
# gridh(0:10); gridv(0:10)     # se vuoi vedere la griglia
x=c(1,10,2); y=c(1,2,6)        # se vuoi cambia triangolo
polyC(x,y,NULL)                # il poligono trasparente
R=incentre(x,y); POINT(R[1],R[2],"brown")
line_line(x[1],y[1], R[1],R[2], x[2],y[2], x[3],y[3])
P1=solut[1]; P2=solut[2]; line(P1,P2, x[1],y[1], "seagreen")
line_line(x[3],y[3], R[1],R[2], x[2],y[2], x[1],y[1])
Q1=solut[1]; Q2=solut[2]; line(Q1,Q2, x[3],y[3], "seagreen")
POINT(R[1],R[2],"red")
# Ho ottenuto la figura iniziale. Posso aggiungere i nomi dei punti
text(x[1]-1/2,y[1],"A"); text(x[2]+1/2,y[2],"B"); text(x[3],y[3]+1/2,"C")
text(P1+1/2,P2+1/2,"P"); text(Q1+1/2,Q2-1/2,"Q"); text(R[1]-3/4,R[2]-0.15,"R")
# I segni per gli angoli, in questo caso particolare
pointD(2.15,5.1,1); pointD(2.8,5.25,1)
ColPoint="green"; pointV(1.5,1.9,1); ColPoint="green"; pointV(1.9,1.4,1)
# il cerchio
circl(R[1],R[2],point_line(R[1],R[2], x[2],y[2], x[1],y[1]), "seagreen")
# la terza bisettrice
line(x[2],y[2],R[1],R[2],"seagreen")
# i tre raggi
perp3p(x[3],y[3], x[2],y[2], R[1],R[2], "red")
perp3p(x[3],y[3], x[1],y[1], R[1],R[2], "red")
perp3p(x[2],y[2], x[1],y[1], R[1],R[2], "red")

Con WoframAlpha:
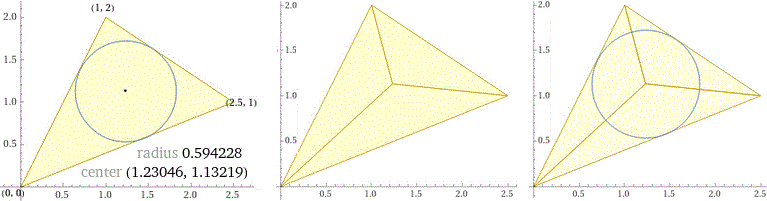
incircle triangle (2.5,1),(1,2),(0,0)
triangle (2.5,1),(0,0),(1.23046,1.13219), triangle (2.5,1),(1,2),(1.23046,1.13219), triangle (0,0),(1,2),(1.23046,1.13219)
polygon (1.23046,1.13219),(2.5,1),(0,0),(1.23046,1.13219),(2.5,1),(1,2),(1.23046,1.13219),(0,0),(1,2), circle center (1.23046,1.13219) radius 0.594228