Il docente può realizzare la figura nel testo dell'esercizio facilmente online con lo script disegnare(4):
vedi (leggi l'help). I comandi (copiabili e incollabili, seguiti da uno spazio bianco o un ";"):
,&40&b&80&1, &40&a&80&2
,&37&b&45&a "1" &20&a "5"
,&45&b&43&a "1" &20&b "5"
,&40&a&40&b &10&c&5&b &10&2 v&10&c&5&bw v&10&d&5&aw &5&7 &10&1
La prima riga traccia gli assi, &40&a&40&b portano nell'origine; ' e " scrivono 1 e 5,
l'ultima riga traccia la figura iniziale.
Ecco come si potrebbe realizzare la figura soluzione:
,&40&b&80&1, &40&a&80&2
,&37&b&45&a "1" &20&a "5"
,&45&b&43&a "1" &20&b "5"
,&40&a&40&b &10&c&5&b &10&2 v&10&c&5&bw v&10&d&5&aw &5&7 &10&1
,&40&a&40&b &20&c&20&b i -
,&40&a&40&b &20&c&20&b v&10&a&5&bw &5&8 &10&2 &10&3 v&10&d&5&cw
,&40&a&40&b &14&cbb &4&2 v&14&cbbw v&4&d&7&aw v&7&cddw &14&1
,&40&a&40&b &20&d&10&a &10&2 v&10&c&5&bw v&10&d&5&aw &5&7 &10&1
,&40&a&40&b &20&a&20&b v&10&c&5&dw &5&6 &10&4 &10&1 v&10&b&5&aw
,&40&a&40&b &5&a&20&b &10&2 &5&7 v&10&c&5&bw v&5&a&10&dw &10&1
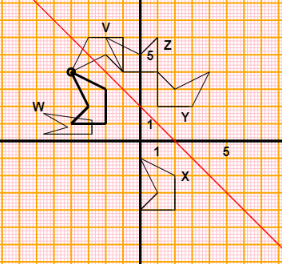
,&40&a&40&b &33&b&10&c V &23&d&20&c W &43&a&20&d X &20&b&3&d Y &21&b&5&c Z
,&80&b&10&a &70& H
Le figure realizzate col software online WolframAlpha, incollando
le immagini via via ottenute coi comandi seguenti:
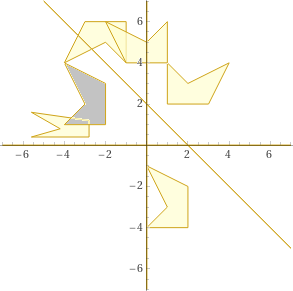
polygon (-4*1.4,0.4),(-2*1.4,0.4),(-2*1.4,3*0.4),(-4*1.4,4*0.4),(-3*1.4,2*0.4); polygon (-4,1),(-2,1),(-2,3),(-4,4),(-3,2); polygon (-7,0),(7,0),(0,0),(0,7),(0,-7),(0,0)
polygon (1,4),(1,2),(3,2),(4,4),(2,3); polygon (0,-4),(2,-4),(2,-2),(0,-1),(1,-3); polygon (-7,0),(7,0),(0,0),(0,7),(0,-7),(0,0)
polygon (-1,4),(-1,6),(-3,6),(-4,4),(-2,5); polygon (1,6),(1,4),(-1,4),(-2,6),(0,5); polygon (-7,0),(7,0),(0,0),(0,7),(0,-7),(0,0)
polygon (-5,7),(7,-5; polygon (-7,0),(7,0),(0,0),(0,7),(0,-7),(0,0)
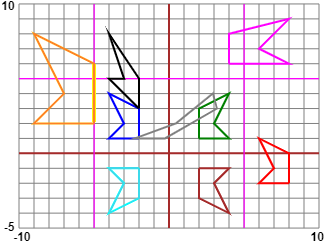 | | Le trasformazioni geometriche
possono essere visualizzate
facilmente anche in JavaScript:
vedi
|
I grafici realizzati con R:
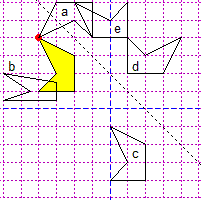 source("http://macosa.dima.unige.it/r.R")
PLANE(-6,5, -5,6)
# Il poligono:
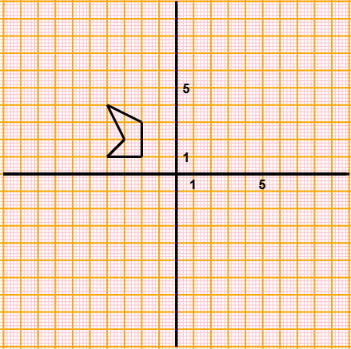
x = c(-2,-2,-4,-3,-4); y = c( 1, 3, 4, 2, 1)
polyC(x,y,"yellow") # Gli altri poligoni non li coloro (uso 0)
polyC(y,-x, 0); text(1.5,2.5,"d",cex=0.8)
polyC(x+4,y-5, 0); text(1.5,-2.5,"c",cex=0.8)
polyC(x*3/2,y/2, 0); text(-5.5,2.5,"b",cex=0.8)
POINT(-4,4,"red")
polyC(-(y-4)-4,x+4+4, 0); text(-2.5,5.5,"a",cex=0.8)
abline(2,-1,lty=3)
polyC(-(y-2),-x+2, 0); text(0.5,4.5,"e",cex=0.8)
source("http://macosa.dima.unige.it/r.R")
PLANE(-6,5, -5,6)
# Il poligono:
x = c(-2,-2,-4,-3,-4); y = c( 1, 3, 4, 2, 1)
polyC(x,y,"yellow") # Gli altri poligoni non li coloro (uso 0)
polyC(y,-x, 0); text(1.5,2.5,"d",cex=0.8)
polyC(x+4,y-5, 0); text(1.5,-2.5,"c",cex=0.8)
polyC(x*3/2,y/2, 0); text(-5.5,2.5,"b",cex=0.8)
POINT(-4,4,"red")
polyC(-(y-4)-4,x+4+4, 0); text(-2.5,5.5,"a",cex=0.8)
abline(2,-1,lty=3)
polyC(-(y-2),-x+2, 0); text(0.5,4.5,"e",cex=0.8)
Idea, ad es. per la rotaz. attorno a (-4,4) di 90°:
porto (-4,4) in (0,0): (x+4, y-4);
ruoto di 90° attorno ad O: (-(y-4), x+4);
faccio la traslazione opposta a quella iniziale: (-(y-4)-4, x+4+4)



 source("http://macosa.dima.unige.it/r.R")
PLANE(-6,5, -5,6)
# Il poligono:
x = c(-2,-2,-4,-3,-4); y = c( 1, 3, 4, 2, 1)
polyC(x,y,"yellow") # Gli altri poligoni non li coloro (uso 0)
polyC(y,-x, 0); text(1.5,2.5,"d",cex=0.8)
polyC(x+4,y-5, 0); text(1.5,-2.5,"c",cex=0.8)
polyC(x*3/2,y/2, 0); text(-5.5,2.5,"b",cex=0.8)
POINT(-4,4,"red")
polyC(-(y-4)-4,x+4+4, 0); text(-2.5,5.5,"a",cex=0.8)
abline(2,-1,lty=3)
polyC(-(y-2),-x+2, 0); text(0.5,4.5,"e",cex=0.8)
source("http://macosa.dima.unige.it/r.R")
PLANE(-6,5, -5,6)
# Il poligono:
x = c(-2,-2,-4,-3,-4); y = c( 1, 3, 4, 2, 1)
polyC(x,y,"yellow") # Gli altri poligoni non li coloro (uso 0)
polyC(y,-x, 0); text(1.5,2.5,"d",cex=0.8)
polyC(x+4,y-5, 0); text(1.5,-2.5,"c",cex=0.8)
polyC(x*3/2,y/2, 0); text(-5.5,2.5,"b",cex=0.8)
POINT(-4,4,"red")
polyC(-(y-4)-4,x+4+4, 0); text(-2.5,5.5,"a",cex=0.8)
abline(2,-1,lty=3)
polyC(-(y-2),-x+2, 0); text(0.5,4.5,"e",cex=0.8)