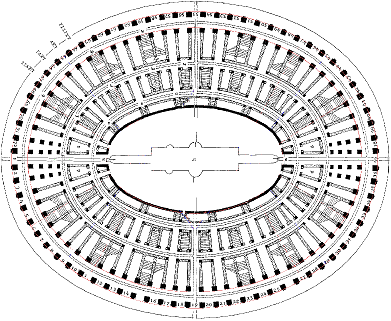
A lato è riprodotta una pianta del Colosseo.  Clicca qui per vederla di dimensioni maggiori.  In qualche pubblicazione si afferma che non ha forma ellittica.  Prova ad individuare con del software l'equazione di una ellisse che abbia semiassi proporzionali a quelli del Colosseo e prova a sovrapporre la sua immagine a quella della pianta del Colosseo.  Che cosa puoi concludere?

Ecco, sotto a sinistra, l'immagine nelle dimensioni originali e, a destra, la lunghezza in pixel dei cosiddetti "asse maggiore" e "asse minore", lette direttamente col software per disegnare (Paint o simili), dopo avervi incollato l'immagine (si potrebbero ottenere valori diversi da questi, ma ad essi proporzionali). Lo facciamo anche per la pista del Colosseo.

 

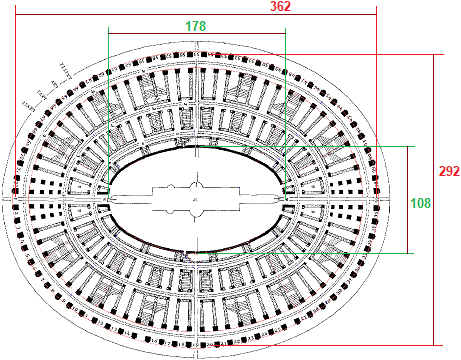
A questo punto tracciamo, ad esempio con WolframAlpha (vedi), una coppia di ellissi aventi tali assi e proviamo a sovrapporle all'immagine del Colosseo, eventualmente modificando le dimensioni del Colosseo agendo col mouse sulla finestra grafica.

Ottima sovrapposizione! Che cosa possiamo concludere? Che bisogna stare attenti alle cose di "matematica" che si trovano scritte da persone che non sono competenti di "matematica" e argomentano usando strumenti di cui non hanno la piena padronanza!

Come trovare i fuochi. Basta introdurre (x/(362/2))^2+(y/(292/2))^2=1 e poi (x/(178/2))^2+(y/(108/2))^2=1 in WolframAlpha per ottenere per la prima (-106.981,0) e (106.981,0), per la seconda (-70.746,0) e (70.746,0)
 

Proviamo a fare tutto anche con R. Tracciamo una coppia di ellissi aventi tali assi e proviamo a sovrapporle all'immagine del Colosseo, eventualmente modificando le dimensioni delle ellissi agendo col mouse sulla finestra grafica.

source("http://macosa.dima.unige.it/r.R")
BF=6; HF=5
a1=362/2; a2=292/2;  b1=178/2; b2=108/2
C1=function(x,y) (x/a1)^2+(y/a2)^2-1
C2=function(x,y) (x/b1)^2+(y/b2)^2-1
PLANE(-190,190,-150,150); CURV(C1,"blue"); CURV(C2,"brown")

 

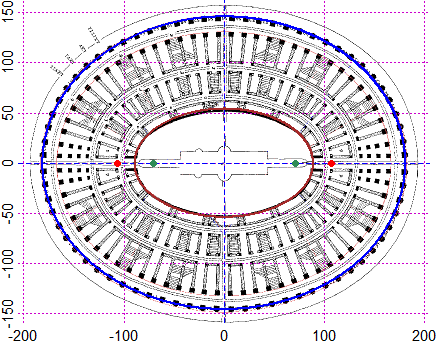
Per trovare i fuochi delle due ellissi ed analizzare altri aspetti uso il comando conic

 conic()
# Use  Conic(w)  where w is c(a,b,c,d,e,f)  for  a*x^2+b*x*y+c*y^2+d*x+e*y+f = 0 
# C1 and, as appropriate, xC,yC, xV,yV, xF,yF, xF1,yF1, xF2,yF2, FV are stored 
co1 = c(1/a1^2,0,1/a2^2,0,0,-1); co2 = c(1/b1^2,0,1/b2^2,0,0,-1)
Conic(co1)
# C1=function(x,y)  3.05241e-05 * x^2 + 0 * x*y + 4.691312e-05 * y^2 + 0 * x + 0 * y + -1 
# ellipse  xC = 0  yC = 0 
# dir.major ax: 0 °  dir.minor ax: 270 ° 
# semi-major axis 181  semi-minor axis 146 
# F1 106.9813 0  F2 -106.9813 0  eccentr 0.5910569 
# Then you have the length of the string that draws the Ellipse with 
# StringE(xF1,yF1, xF2,yF2)   [which is = major axis = distance V1-V2]
# and the vector from F1 to V1 (or from F2 to V2) with  FV
POINT(xF1,yF1,"red"); POINT(xF2,yF2,"red")
# Calcoliamo anche la lunghezza della corda con cui tracciare l'ellisse
StringE(xF1,yF1, xF2,yF2)
# 362    (che è eguale alla distanza tra V1 e V2)
Conic(co2)
# C1=function(x,y)  0.0001262467 * x^2 + 0 * x*y + 0.0003429355 * y^2 + 0 * x + 0 * y + -1 
# ellipse  xC = 0  yC = 0 
# dir.major ax: 0 °  dir.minor ax: 270 ° 
# semi-major axis 89  semi-minor axis 54 
# F1 70.74602 0  F2 -70.74602 0  eccentr 0.7948992 
# ...
POINT(xF1,yF1,"seagreen"); POINT(xF2,yF2,"seagreen")

Ritrovo (ovviamente, in quanto le ho usate per definire le due curve) anche le lunghezze degli assi delle 2 ellissi:   181*2 = 362, 146*2 = 292,   89*2 = 178, 54*2 = 108. La lunghezza della curva è 362

Quali sono i vertici verticali e orizzontali dell'ellisse?  Sono, come è facile trovare anche intersecando con x=0 e con y=0 la curva, (0,a2), (0,-a2), (a1,0), (-a1,0).  Li tracciamo.

POINT(0,a2, "brown"); POINT(0,-a2, "brown"); POINT(a1,0, "magenta"); POINT(-a1,0, "magenta")

Tracciamo l'ellisse anche in modo diverso, descrivendola come punti che hanno somma delle distanze dai fuochi costante. Questa somma vale 2·a1 = 2·181. Infatti la somma della distanza di (a1,0) da F1 e di quella da F2 è eguale alla distanza di (a1,0) da (a2,0). Nella figura seguente è stata tracciate in verde chiaro.  In verde mare è stata tratteggiata anche la spezzata che congiunge i fuochi con un punto dell'ellisse.

X=function(t) cos(t)*a1; Y=function(t) sin(t)*a2
par1(X,Y, 0,2*pi, "green")
t=pi/4; POINT(X(t),Y(t),"brown")
coldash="seagreen"; segm(xF1,0, X(t),Y(t),0); segm(xF2,0,X(t),Y(t),0)