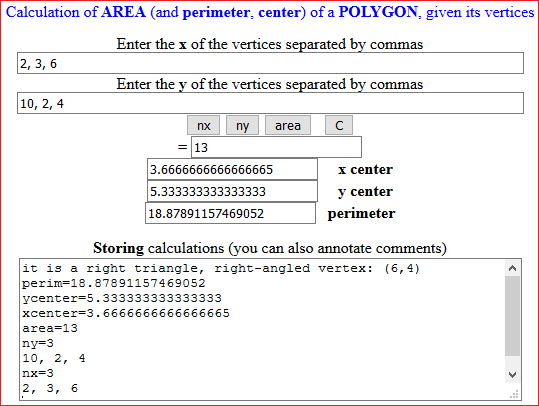
Siano: A = (-4,0), B = (-2,4), C = (4,-1), D = (2,10), E = (3,2), F = (6,4).
Senza disegnarli, stabilisci quale o quali dei triangoli ABC e DEF sono rettangoli.
Possiamo ragionare, ad es., confrontando le pendenze dei lati o verificando se vale la relazione pitagorica.
ABC - primo metodo
Pendenza di AB: 4/2 = 2, di BC: -5/6, di AC: -1/8. In nessun caso abbiamo due pendenze in cui una sia l'opposto del reciproco dell'altra (ossia il cui prodotto sia -1). Quindi ABC non è rettangolo.
ABC - secondo metodo
d(A,B)2 = 42+22 = 20; d(B,C)2 = 52+62 = 61; d(A,C)2 = 12+82 = 65.
Nessuno dei valori ottenuti è la somma degli altri due, per cui non siamo di fronte a un triangolo rettangolo.
DEF - primo metodo
Pendenza di DE: -8/1, di EF: 2/3, di DF: -6/4 = -3/2. EF e DF sono dunque perpendicolari (e DE non è parallelo - e non è quindi allineato - ad essi, a conferma che
si tratta effettivamente di un triangolo). Quindi siamo di fronte a un triangolo rettangolo.
DEF - secondo metodo
d(D,E)2 = 82+12 = 65, d(E,F)2 = 22+32 = 13; d(D,F)2 = 62+42 = 52.
65 = 52+13. Siamo dunque di fronte a un triangolo rettangolo.
Volendo, posso controllare l'esercizio con questo script online.
Per altre eventuali osservazioni: 
figure (2) e
distanza (e
triangoli)
neGli Oggetti Matematici.
Con WolframAlpha posso anche tracciare i triangoli:
angles of triangle (-4,0),(-2,4),(4,-1), angles of triangle (2,10), (3,2), (6,4)
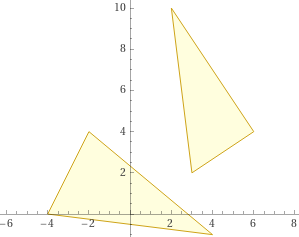
1º (0.570383 rad | 1.2315 rad | 1.33971 rad)
2º (π/2 rad | 0.463648 rad | 1.10715 rad) (π/2 rad = 90°)
Altra figura:
tracciata con lo script online disegnare(5): vedi (leggi l'help). I comandi (copiabili e incollabili, seguiti da uno spazio bianco o un ";"):
, &5&a &15&2, &5&b &15&1 :
,&5&a&5&b &4&c v&2&a&4&bw v&6&a&5&dw v&8&cbw
,&5&a&5&b &3&a&2&b v&3&a&2&bw v&4&c&6&bw v&1&a&8&dw