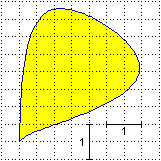
Misura (approssimativamente) l'area della figura a sinistra (indica la precisione della misura che hai effettuato)
| | Misura (approssimativamente) l'area della figura a sinistra (indica la precisione della misura che hai effettuato) |
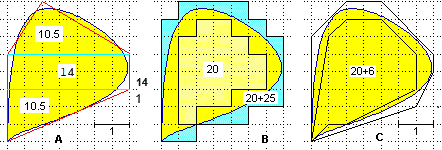
| Vi sono varie strategie. Quella raffigurata sotto in A consiste nell'approssimare il contorno con una figura poligonale e nel valutare l'entità dell'errore considerando quanto le parti indebitamente incluse compensano quelle escluse: l'area del poligono è 35 quadretti; l'errore si può stimare in al più 2 quadretti; quindi l'area sarebbe 35±2 quadretti; poichè un quadretto ha area 1/4, l'area è 8.75±0.5. Il metodo illustrato in B è più semplice: l'area è compresa tra 20 e 45 quadretti, cioè tra 5 e 11.25 (non contrasta con la precedente valutazione: questo intervallo di misure include il precedente). Il metodo in C cerca di precisare le valutazioni per difetto ed eccesso fatte in B considerando e mettendo insieme anche frazioni di quadretto (la parte interna verrebbe 26 quadretti, cioè 6.5; anlogamente si può valutare l'area del poligono contenitore). |
 |
Ma avrei potuto anche triangolare la figura e ricavare le aree dei triangoli dalle lunghezze dei lati:
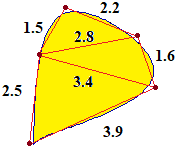
Per calcolare le aree dei triangoli posso ricorrere ad uno script: script
ottenendo 1.6393119745796, 2.2211483516416 e 4.2, la cui somma è 8.0604603262212, arrotondabile a 8.1. Ovvero posso utilizzare
WolframAlpha:
area triangle (1.5,2.2,2.8) → 1.63931 area triangle (3.4,1.6,2.8) → 2.22115 area triangle (3.4,2.5,3.9) → 4.2
1.63931 + 2.22115 + 4.2 → 8.06046 (che arrotondo a 8.1).
Ovvero potevo usare R:
source("http://macosa.dima.unige.it/r.R")
AREAT(1.5,2.2,2.8)+AREAT(2.8,1.6,3.4)+AREAT(3.4,3.9,2.5)
In alternativa, utilizzando R, potevo stimare le coordinate di un po' di punti e utilizzare le "spline" per approssimare il contorno e, quindi, valutare l'area (vedi):
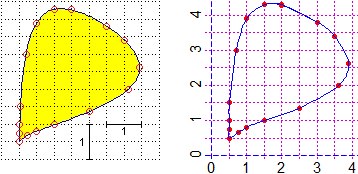
x=c(0.5,0.75,1,1.5,2.5,3.62,3.9,3.5,3,2,1.5,1,0.7,0.51,0.5,0.5) y=c(0.5,0.65,0.8,1,1.35,2,2.62,3.4,3.8,4.29,4.29,3.9,3,1.5,1,0.75) PLANE(0, 4.3, 0, 4.3); gridh((0:4)+1/2); gridv((0:4)+1/2) Point(x,y,"red") polyl(splineCx(x,y),splineCy(x,y),"blue") areaPol(splineCx(x,y),splineCy(x,y)) # 8.443126 Prendo 8.4 come approssimazione
Ovvero con WolframAlpha posso utilizzare:
polygon(.5,.5),(.75,.65),(1,.8),(1.5,1),(2.5,1.35),(3.63,2),(3.9,2.62),(3.5,3.4),(3,3.8),(2,4.3),(1.5,4.3),(1,3.9),(.7,3),(.51,1.5),(.5,1),(.5,.75)
ottenendo 8.26255, che arrotondo a 8.3 ± 1.
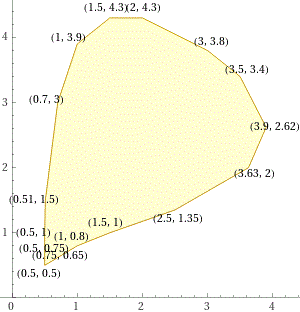
Posso anche ricorrere direttamente da rete allo script areaPol ottenendo (più o meno con gli stessi punti, ma potrei aggiungerne quanti voglio):
che arrontondo a 8.3.
Con lo script disegnare(4): vedi (leggi l'help) si può anche tracciare la figura:
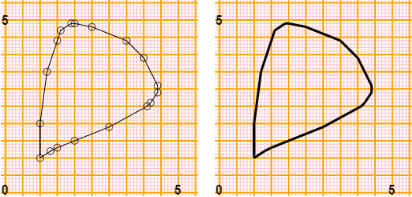
, b"0"&50&a"5", &50&b"5"
,-&10&a &10&b vaaabbwi vaabwi v&5&abbwi v&10&a&4&bwi v&11&a&6&bwi vabwi vaabbbwi vbbwi v&4&c&8&bwi v&5&c&5&bwi v&10&c&4&bwi v&5&cbwi vcwi vcccddwi vcdddwi v&9&dcccwi v&15&dccwi &10&4i
, b"0"&50&a"5", &50&b"5"
, &10&a &10&b vaaabbw vaabw v&5&abbw v&10&a&4&bw v&11&a&6&bw vabw vaabbbw vbbw v&4&c&8&bw v&5&c&5&bw v&10&c&4&bw v&5&cbw vcw vcccddw vcdddw v&9&dcccw v&15&dccw &10&4
Per altri commenti: 
approssimazioni, calcolo approssimato e area neGli Oggetti Matematici.