| (1) Dispositivi
simili sono molto comuni
(transenne, sottotegami, … di ampiezza regolabile, elevatori,
…). Se ci proponiamo di disegnare questi o
altri meccanismi articolati incontriamo subito qualche difficoltà.
Non basta tentare di riprodurre più o meno la forma di ciò
che si è visto per realizzare il disegno, ma
occorre aver compreso le relazioni che
intercorrono tra i diversi elementi che
lo compongono. |
 |
Ciò
vale più in generale per la
lettura/interpretazione/memorizzazione di ogni tipo di immagine.
Quando osserviamo una figura come quella a fianco noi la
interpretiamo come una piramide, non come una coppia di triangoli,
e alla richiesta di disegnare un'altra figura dello stesso tipo
realizziamo il disegno facendo riferimento non direttamente alle
componenti del disegno, ma al concetto
di piramide di cui in qualche modo abbiamo già costruito una
rappresentazione mentale. Quando osserviamo una situazione complessa
(disegno o immagine dal vivo) nel memorizzarla la riorganizziamo
associandola ad altre immagini, scorporandola e riaggregandola usando
ricordi visivi di situazioni "prototipo", associazioni
mentali, … , filtrando (più o meno consapevolmente) le
cose che maggiormente ci interessano, …. I nostri ricordi, ma
anche i nostri sguardi, non sono oggettivi: non guardiamo
solo con i sensi, ma con il complesso del cervello [ Prospettiva negli Oggetti Matematici]. Prospettiva negli Oggetti Matematici]. |
|
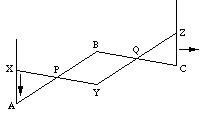
Per capire il funzionamento del dispositivo è utile pensarlo in movimento (vedi la figura a destra).
Si capisce che i perni P e Q sono a metà delle aste AB e XY, YZ e BC. Si capisce anche che AB = YZ e XY = BC.
(2) Formalizzando, una proprietà geometrica che motiva il buon funzionamento del dispositivo potrebbe essere:
Se AB=YZ, XY=BC, P appartiene
ad AB e a XY, Q appartiene a BC e a YZ, AP=PB, XP=PY, BQ=QC e YQ=QZ,
allora la retta AX è parallela alla retta CZ.
|
 |
(3) Una spiegazione intuitiva è la seguente:
le aste AB e XY sono imperniate a metà; i perni A e X non possono muoversi in orizzontale; quindi i perni B e Y, a partire dalla posizione "iniziale", avanzano orizzontalmente entrambi il doppio di quanto avanza il perno P; con un ragionamento analogo si conclude che C e Z avanzano orizzontalmente della stessa distanza rispetto a B e Y, e in tutto il quadruplo di quanto è avanzato P. Si può anche concludere che la massima distanza in orizzontale raggiungibile è pari a 4 volte la lunghezza di XP (o di AP, se questo fosse più breve di XP) , cioè 2 volte XY. La figura a destra precisa la proprietà geometrica intuitiva su cui si basa l'argomentazione:
se si ruota un'asta, i punti di essa assumono distanze dalla posizione iniziale dell'asta proporzionali alle loro distanze dal perno. |
 |
La dimostrazione matematica è semplice: modellizzo la situazione assumendo il perno attorno a cui l'asta ruota come origine degli assi; al ruotare della retta su cui sta l'asta i punti di essa hanno variazioni x e y che si mantengono tra loro proporzionali.
Dunque sia B che Y hanno distanza da AX doppia di quella che ha P; essendo equidistanti da AX individuano una retta parallela ad AX. Analogamente Z e C hanno uguale distanza da BY e quindi individuano una retta parallela a BY. CZ ha la stessa inclinazione di BY che ha la stessa inclinazione di AX: AX e CZ sono quindi parallele.
Era possibile anche procedere rappresentando tutta la situazione su un sistema di riferimento, assumendo A come origine e AX come asse y, ed ottenere che BY è la retta x=2xP e CZ è la retta x=4xP , che è parallela all'asse y (ossia ad AX).
Si poteva, infine, procedere considerando il segmento BY simmetrico ad AX rispetto al centro di simmetria P; le simmetrie centrali non sono altro che rotazioni di 180°, quindi trasformano una retta in una retta ad essa parallela; la retta BY è dunque parallela ad AX. Analogamente CZ è parallela a BY e, per la proprietà transitiva, lo è anche ad AX.
|
Queste dimostrazioni sono facili in un approccio alla geometria in cui le rette sono introdotte "vettorialmente", come generate da un punto che si muove in una direzione fissata. Questo è l'approccio usato negli  Oggetti Matematici. Oggetti Matematici.
In altri approcci (come quello del manuale di Enriques ed Amaldi) è necessario scomporre la figura in triangoli e ragionare su di essi, in modo meno direttamente legato all'intuizione "dinamica". Ecco una possibile dimostrazione:
|







