I "tetrapack" sono contenitori a forma di tetraedro regolare. Sono costruiti a partire da un cilindro, come illustrato nella figura a lato. Se il diametro del cilindro è 12 cm, qual è il volume del "tetrapack"?
Vedi qui per i poliedri regolari, di cui il tetraredro regolare è uno dei 5 tipi.  Come si capisce dalla figura soprastante a destra, lo spigolo del tetraedro è pari al diametro del cilindro.

Sotto a sinistra lo sviluppo del tetraedro, che ha "quattro" facce (tetr- deriva dal greco téssares, quattro).  Esse sono dei triangoli equilateri (figura al centro a sinistra).
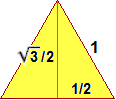
Indichiamo con s la lunghezza dello spigolo.  L'area A di una faccia (figura al centro a destra) è l'area di un triangolo equilatero di lato s, ossia √3/4·s².  Dobbiamo trovare h; sappiamo che è √(s²−k²).
s/2 (figura al destra) è √3/2·k, ovvero k = s/√3; quindi h = √(s²−s²/3) = s·√(2/3)
Il volume è quindi A·h/3 = √3/4·s²·s·√(2/3)/3 = s³·√2/12 = 203.64675298… cm³ = 204 cm³, ossia poco più di 200 cm³.  È un cartoccio usato per contenere 1/5 di litro.