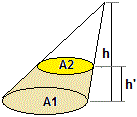
Un tronco di cono ha la base maggiore di 237 centimetri quadrati. Le due basi stanno in piani che distano 12.4 centimetri. Il cono originale, prima del "troncamento", era alto 27.8 cm. Qual è il volume del tronco di cono?

Siano L1 ed L2 i diametri o le lunghezze di due segmenti che stanno sulle basi A1 ed A2 raffigurate e che sono proiettati l'uno nell'altro dal vertice del cono.  Abbiamo che, per la similitudine dei triangoli aventi L1 ed L2 come basi ed h e h' come altezze,   L1/L2 = h/(h−h').  Inoltre  A1/A2 = (L1/L2)².  Il tronco di cono ha volume  A1·h/3−A2·(h−h')/3, ossia (A1·h−A2·(h−h'))/3. Io conosco h', h ed A1.  Posso ricavare A2 dalle prime due equazioni. A2 = A1/(L1/L2)² = A1/(h/(h−h'))² Posso dunque ottenere:

A1 <- 237; h1 <- 12.4; h <- 27.8
A2 <- A1/(h/(h-h1))^2; A2
# 72.72776
# (OK: il rapporto tra h e h' è circa 2, quindi tra A1 e A2 è circa 4) 
(A1*h-A2*(h-h1))/3
# 1822.864

Volendo, avendola sottomano, potevo usare la formula che esprime il volume del tronco di cono (e di piramide) in funzione di A1, A2 e h' ( volume): (A1+√(A1·A2)+A2)·h'/3.
Come prima trovo che il rapporto tra le lunghezze di segmenti corrispondenti sulle due facce è pari ad h/(h−h'), quello tra le aree è il suo quadrato.  Quindi A2 = A1/h/(h−h')².  Il volume dunque è
(A1+sqrt(A1*A2)+A2)*h1/3
# 1822.864
ossia 1.820 dm³, quasi 2 litri.