Il valore calorico di proteine, grassi e glucidi è, rispettivamente, 4.1, 9.3 e 4.1 kcal/g. La tabella A indica la percentuale (ovvero il numero di grammi per 100 grammi di sostanza) di proteine, grassi e glucidi (1ª, 2ª, 3ª colonna) del pane, dei gamberetti e della maionese che una azienda impiega per produrre dei tramezzini. La azienda vuole combinare gli ingredienti in modo da produrre tramezzini che contengano ciascuno 12 g di proteine, 15 g di grassi e 40 g di glucidi.
Siano:
(1) Che cosa rappresentano le espressioni seguenti?
A·B Ct·B At·X = C S·X
(la trasposta Mt di M m×n è la matrice n×m ottenuta scambiando righe e colonne: Mt[i,j] = M[j,i])
(2) Risolvi il problema della azienda.
# A è 3*3, B 3*1, A*B è 3*1:
/8 1 55\ /4.1\ / 8*4.1+ 1*9.3+55*4.1\ /267.6\ /270\
|14 1 3| * |9.3| = | 14*4.1+1*9.3+3*4.1 | = | 79 | = | 80|
\1 80 3/ \4.1/ \ 1*4.1+80*9.3+3*4.1 / \760.4/ \760/
arrotond.
Sono le Chilocalorie fornite da 1 hg di ciascuna sostanza.
# C è 3*1, Ct è 1*3, Ct*B è 1*1:
/4.1\
(12 15 90) * |9.3| = (12*4.1+15*9.3+90*4.1) = (352.7) = (350)
\4.1/ arrotond.
Sono le Chilocalorie fornite da 1 tramezzino.
# At è 3*3 come A; X è 3*1; At*X è 3*1 come C.
/8 14 1\ /p\ /12\
|1 1 80| * |g| = |15|
\55 3 3/ \m/ \40/ equivale a:
8p + 14g + m = 12
p + g + 80m = 15
55p + 3g + 3m = 40 È il sistema di equazioni che è il
modello del problema della ditta;
p, g e m sono il peso in hg dei tre ingredienti.
# S è 1*3, X è 3*1, S*X è 1*1:
/p\
(1 1 1) * |g| = (p+g+m) è il peso in hg di 1 tramezzino
\m/
# Per risolvere il sistema At*X = C se usiamo un programma in
grado di effettuare calcoli matriciali eseguiamo (At)-1*C.
/.6933568\ /0.69\
Si ottiene: |.4485657| = |0.45| È il peso in hg dei
\.173226 / \0.17/ tre ingredienti
[Cliccando  QUI, puoi accedere ad R che ti consente
di svolgere il calcolo matriciale]
# Oppure si può usare la regola di Cramer
|8 14 1| |12 14 1|
|1 1 80| = 59610 |15 1 80| = 41331
|55 3 3| |90 3 3|
p = 41331/59610 = 0.69; in modo analogo si trovano g e m
# Oppure si può procedere manipolando il sistema
# Come risolvere il sistema con questo semplice script online
# (che puoi anche scaricare sul computer):
QUI, puoi accedere ad R che ti consente
di svolgere il calcolo matriciale]
# Oppure si può usare la regola di Cramer
|8 14 1| |12 14 1|
|1 1 80| = 59610 |15 1 80| = 41331
|55 3 3| |90 3 3|
p = 41331/59610 = 0.69; in modo analogo si trovano g e m
# Oppure si può procedere manipolando il sistema
# Come risolvere il sistema con questo semplice script online
# (che puoi anche scaricare sul computer):
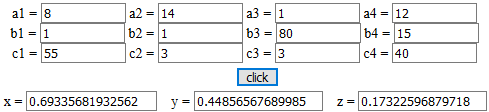 - - - - - - - - - - - - - - - - - - - - - - - - -
# I calcoli con R
A <- matrix(data=c(8,14,1,1,1,80,55,3,3), nrow=3, ncol=3); A
# [,1] [,2] [,3]
# [1,] 8 1 55
# [2,] 14 1 3
# [3,] 1 80 3
B <- matrix( data=c(4.1,9.3,4.1), nrow=3, ncol=1); B
# [,1]
# [1,] 4.1
# [2,] 9.3
# [3,] 4.1
A %*% B
# [,1]
# [1,] 267.6
# [2,] 79.0
# [3,] 760.4
C <- matrix( data=c(12,15,40), nrow=3, ncol=1); C
# [,1]
# [1,] 12
# [2,] 15
# [3,] 40
t(C) %*% B
# [,1]
# [1,] 352.7
library(MASS)
ginv(t(A)) %*% C
# [,1]
# [1,] 0.6933568
# [2,] 0.4485657
# [3,] 0.1732260
# NOTA: potevo anche specificare i nomi di righe e colonne
nomA <- list(c("pane","gamberetti","maionese"),c("proteine","grassi","glucidi"))
A <- matrix(data=c(8,14,1,1,1,80,55,3,3), nrow=3, ncol=3, dimnames=nomA); A
nomB <- list(c("CalPr","CalGr","CalGl"))
B <- matrix( data=c(4.1,9.3,4.1), nrow=3, ncol=1, dimnames=nomB); B
nomC <- list(c("GrPr","GrGr","GrGl"))
C <- matrix( data=c(12,15,40), nrow=3, ncol=1, dimnames=nomC); C
t(C) %*% B
library(MASS)
ginv(t(A)) %*% C
# ovvero:
matrix( ginv(t(A)) %*% C, dimnames=list(c("pane","gamberetti","maionese")))
#
# Alternativa, per la soluzione del sistema:
source("http://macosa.dima.unige.it/r.R")
S = c(8,14,1, 12, 1,1,80, 15, 55,3,3, 40); sistema(S)
# 0.6933568 0.4485657 0.1732260
#
# Ovvero si possono usare questi script online.
- - - - - - - - - - - - - - - - - - - - - - - - -
# I calcoli con R
A <- matrix(data=c(8,14,1,1,1,80,55,3,3), nrow=3, ncol=3); A
# [,1] [,2] [,3]
# [1,] 8 1 55
# [2,] 14 1 3
# [3,] 1 80 3
B <- matrix( data=c(4.1,9.3,4.1), nrow=3, ncol=1); B
# [,1]
# [1,] 4.1
# [2,] 9.3
# [3,] 4.1
A %*% B
# [,1]
# [1,] 267.6
# [2,] 79.0
# [3,] 760.4
C <- matrix( data=c(12,15,40), nrow=3, ncol=1); C
# [,1]
# [1,] 12
# [2,] 15
# [3,] 40
t(C) %*% B
# [,1]
# [1,] 352.7
library(MASS)
ginv(t(A)) %*% C
# [,1]
# [1,] 0.6933568
# [2,] 0.4485657
# [3,] 0.1732260
# NOTA: potevo anche specificare i nomi di righe e colonne
nomA <- list(c("pane","gamberetti","maionese"),c("proteine","grassi","glucidi"))
A <- matrix(data=c(8,14,1,1,1,80,55,3,3), nrow=3, ncol=3, dimnames=nomA); A
nomB <- list(c("CalPr","CalGr","CalGl"))
B <- matrix( data=c(4.1,9.3,4.1), nrow=3, ncol=1, dimnames=nomB); B
nomC <- list(c("GrPr","GrGr","GrGl"))
C <- matrix( data=c(12,15,40), nrow=3, ncol=1, dimnames=nomC); C
t(C) %*% B
library(MASS)
ginv(t(A)) %*% C
# ovvero:
matrix( ginv(t(A)) %*% C, dimnames=list(c("pane","gamberetti","maionese")))
#
# Alternativa, per la soluzione del sistema:
source("http://macosa.dima.unige.it/r.R")
S = c(8,14,1, 12, 1,1,80, 15, 55,3,3, 40); sistema(S)
# 0.6933568 0.4485657 0.1732260
#
# Ovvero si possono usare questi script online.
























 QUI, puoi accedere ad R che ti consente
di svolgere il calcolo matriciale]
# Oppure si può usare la regola di Cramer
|8 14 1| |12 14 1|
|1 1 80| = 59610 |15 1 80| = 41331
|55 3 3| |90 3 3|
p = 41331/59610 = 0.69; in modo analogo si trovano g e m
# Oppure si può procedere manipolando il sistema
# Come risolvere il sistema con questo semplice script online
# (che puoi anche scaricare sul computer):
QUI, puoi accedere ad R che ti consente
di svolgere il calcolo matriciale]
# Oppure si può usare la regola di Cramer
|8 14 1| |12 14 1|
|1 1 80| = 59610 |15 1 80| = 41331
|55 3 3| |90 3 3|
p = 41331/59610 = 0.69; in modo analogo si trovano g e m
# Oppure si può procedere manipolando il sistema
# Come risolvere il sistema con questo semplice script online
# (che puoi anche scaricare sul computer):
