Siano A, B e C matrici (quadrate o no, a seconda dei casi) e k un numero reale. Quali tra le seguenti equazioni sono vere per ogni scelta delle matrici? Quando esistono scelte per cui sono false si descrivano una di queste scelte e, se esiste, una scelta in cui siano vere. Eventualmente si sostituisca il termine destro con un'altro che renda l'equazione sempre vera.
[per fare tentativi su cui ragionare può essere utile usare un programma, ad es. R]
  (1) A+B = B+A    (2) (A+B)+C = A+(B+C)    (3) (A+B)+C = (C+A)+B
  (4) kA+A = (k+1)A    (5) (A+B)t = At+Bt    (6) det(kA) = k·det(A)
  (7) det(A+B) = det(A)+det(B)    (8) C·(A+B) = C·A+C·B
  (9) A·B = B·A    (10) (A·B)·C =A·(B·C)    (11) A·(kB) = k(A·B)
  (12) (A·B)–1 = A–1·B–1    (13) (A·B)t = At·Bt    (14) det(At) = det(A)
  (15) det(A·B) = det(A)·det(B)      (16) det(A–1) = det(A)    (17) (At)–1 = (A–1)t

(1), (2), (3), (4), (5), (8), (10), (11), (14), (15), (17) sono sempre vere (Nota: dalla 15 non discende che det(A*B)=det(B*A); ciò vale solo se A e B sono matrici quadrate). Vediamo come ad es. si potrebbero congetturare la (16) [corretta - vedi sotto] e la (17) usando il programma indicato: 

library(MASS); A <- runif(4); M <- array(data=A, dim=c(2,2))
# matrice, trasposta, inversa
M; t(M); ginv(M)
#           [,1]      [,2]
# [1,] 0.1377606 0.2232675
# [2,] 0.4347845 0.5287561
#           [,1]      [,2]
# [1,] 0.1377606 0.4347845
# [2,] 0.2232675 0.5287561
#           [,1]      [,2]
# [1,] -21.82101  9.213931
# [2,]  17.94293 -5.685181
det(M); det(ginv(M)); det(M)*det(ginv(M))
# [1] -0.02423149
# [1] -41.26861
# [1] 1
#  OK
t(ginv(M)); ginv(t(M))
#            [,1]      [,2]
# [1,] -21.821009 17.942933
# [2,]   9.213931 -5.685181
#            [,1]      [,2]
# [1,] -21.821009 17.942933
# [2,]   9.213931 -5.685181
#  OK
La (6) varrebbe sostituendo il secondo termine con k2det(A) se A è 2×2, con kndet(A) se A è n×n; vale quindi sicuramente quando k=1 o det(A)=0 e mai se k 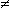1 e det(A) 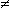0.
La (7) vale se B = k*A per qualche numero k. Per un controesempio si pensi ad A con prima riga (1,0) e seconda riga (0,0), B con prima riga (0,0) e seconda (0,1). det(A)=det(B)=0, det (A+B)=1.
La (9) non vale sicuramente se A e B non sono quadrate: A*B e B*A hanno dimensioni diverse. Per un controesempio nel caso di matrici quadrate si pensi ad A con prima riga (1,0) e seconda riga (0,0), B con prima riga (0,1) e seconda (0,0). A*B=B, B*A=0.
La (12) varebbe sostituendo il secondo termine con B–1*A–1; infatti A*B*B–1*A–1 = A*(B*B–1)*A–1 = A*I*A–1 = A*A–1 = I (I matrice identità). Così com'è vale sicuramente quando A*B è uguale a B*A. È facilissimo trovare controesempi.
La (13) varebbe sostituendo il secondo termine con Bt*At. Così com'è vale sicuramente quando A*B è uguale a B*A. È facilissimo trovare controesempi.
La (16) varebbe sostituendo il secondo termine con 1/det(A). Così com'è vale solo quando |det(A)|=1.