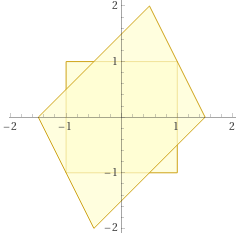
Data la matrice A, la funzione F e il quadrato seguenti,
(a) traccia il trasformato del quadrato mediante F,
(b) traccia il sistema di riferimento i cui versori degli assi sono i trasformati mediante F dei versori del sistema di riferimento di partenza,

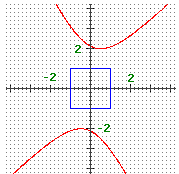
(c) determina l'equazione che rappresenta nel piano x,y la curva raffigurata a lato, che nel piano X,Y ha equazione XY=1.
A =  ⎧ ⎩ 1     -1/2 ⎫ ⎭ 1 1     F ⎧ ⎩ x ⎫ ⎭  = A ×  ⎧ ⎩ x ⎫ ⎭ y y

(a,b)  F(x,y) = (x-y/2, x+y) trasforma (1,1) in (1/2,2), (-1,1) in (-3/2,0), (-1,-1) in (-1/2,-2) e (1,-1) in (3/2,0), come illustrato nella figura a fianco, sulla quale sono tracciati anche i versori (F(1,0) = i+j e F(0,1) = -1/2i+j) del nuovo sistema di riferimento. (c)  La matrice A esprime le vecchie coordinate x,y in funzione delle nuove X,Y; quindi dobbiamo fare la sostituzione x = X-Y/2, y = X+Y nella equazione (2/3x + y/3)(-2/3x + 2/3y)=1; otteniamo: (2/3(X-Y/2) + (X+Y)/3)(-2/3(X-Y/2) + 2/3(X+Y))=1 (2/3X - Y/3 + X/3 + Y/3)(-2/3X + Y/3 + 2/3X + 2/3Y)=1 X·Y=1   questa è l'equazione della curva (è un'iperbole) nel nuovo sistema.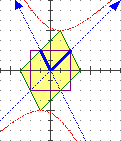

Nota che i punti (1,1) e (-1,-1) nel piano X,Y dell'iperbole sono due vertici del quadrato trasformato. Se trasformassimo la curva (espressa nel piano x,y) con la trasformazione associata alla inversa di A otterremmo la curva x·y=1, ossia l'usuale iperbole equilatera.

[per considerazioni più generali puoi vedere qui]

I poligoni tracciati col software online WolframAlpha:

polygon {(-1,-1),(1,-1),(1,1),(-1,1)}; polygon {(-1+1/2,-2),(1+1/2,0),(1-1/2,1+1),(-1-1/2,1-1)}