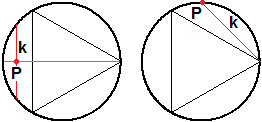
Voglio valutare la probabilità che, prendendo del tutto a caso una corda in un cerchio, la sua lunghezza superi la lunghezza del lato di un triangolo equilatero inscritto in esso. Il problema così è mal posto. Devo precisare come prendo la corda. Calcola la probabilità nel caso in cui  (1) si proceda prendendo le corde perpendicolari ad un diametro e individuandole con il punto di intersezione con esso  e in quello in cui  (2) si fissi un estremo delle corde e le si individui con il loro secondo estremo.

Se procedo nel primo modo devo valutare in quali casi la lunghezza k della corda è maggiore del lato del triangolo. Facendo riferimento alla prima figura a destra, in cui abbiamo preso il raggio lungo 1, k supera il lato del triangolo quando si è nella zona gialla.  Questa è larga 1 infatti (vedi la seconda figura):  il lato verticale del triangolo dista 1/2 dal centro del cerchio, e 1/2+1/2 = 1.  Il punto P pu variare in un intervallo lungo 2, quindi la probabilità è 1/2.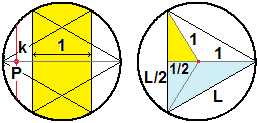

Se procedo nel secondo modo il punto P può variare in un tratto lungo 2π, quanto la circonferenza, mentre la lunghezza della corsa supera L solo quando P sta nel terzo centrale della circonferenza.  Quindi la probabilità è 1/3.

Questo esempio mette in luce come i problemi probabilistici devono essere formulati in modo esauriente, specificando il modo in cui varia il fenomeno casuale (esempi di questo genere furono messi a punto dal francese Bertrand, nel 19º secolo).

Posso studiare il problema anche simulando il fenomeno con un programmino in JavaScript, software che è incorporato in tutti i browser. Basta andare qui: http://macosa.dima.unige.it/js/js.htm (puoi vedere anche qui), cliccare "macosa.dima.unige.it/js.com" e mettere nella finestra in alto:

<pre><script> with(Math) {
L=sqrt(3); M=L/2
n=1e4; s=0; for(i=1;i<=n;i=i+1) {x=random()*2-1; if(sqrt(1-x*x)>M) s=s+1}
document.writeln(s/n)
n=n*10; s=0; for(i=1;i<=n;i=i+1) {x=random()*2-1; if(sqrt(1-x*x)>M) s=s+1}
document.writeln(s/n)
n=n*10; s=0; for(i=1;i<=n;i=i+1) {x=random()*2-1; if(sqrt(1-x*x)>M) s=s+1}
document.writeln(s/n)
} </script></pre>

0.5034
0.49965
0.500012   ->   1/2

<pre><script> with(Math) {
L=sqrt(3); M=L/2
n=1e4; s=0; for(i=1;i<=n;i=i+1) {a=random()*2*PI; if(sqrt(pow(1-cos(a),2)+pow(sin(a),2))>L) s=s+1}
document.writeln(s/n)
n=n*10; s=0; for(i=1;i<=n;i=i+1) {a=random()*2*PI; if(sqrt(pow(1-cos(a),2)+pow(sin(a),2))>L) s=s+1}
document.writeln(s/n)
n=n*10; s=0; for(i=1;i<=n;i=i+1) {a=random()*2*PI; if(sqrt(pow(1-cos(a),2)+pow(sin(a),2))>L) s=s+1}
document.writeln(s/n)
} </script></pre>

0.332
0.33237
0.333     ->   1/3

Come si potrebbe studiare il problema con simulazioni realizzate con R:

L <- sqrt(3); M <- L/2
n <- 1e4; s <- 0; for(i in 1:n) {x <- runif(1)*2-1; s <- s+ifelse(sqrt(1-x^2)>M,1,0)}; s/n
# 0.5021
n <- 1e5; s <- 0; for(i in 1:n) {x <- runif(1)*2-1; s <- s+ifelse(sqrt(1-x^2)>M,1,0)}; s/n
# 0.50069
#
n <- 1e4; s <- 0; for(i in 1:n) {a <- runif(1)*2*pi; s <- s+ifelse(sqrt((1-cos(a))^2+sin(a)^2)>L,1,0)}; s/n
# 0.3389
n <- 1e5; s <- 0; for(i in 1:n) {a <- runif(1)*2*pi; s <- s+ifelse(sqrt((1-cos(a))^2+sin(a)^2)>L,1,0)}; s/n
# 0.33221