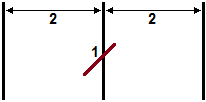
Una superficie piana è percorsa da rette parallele distanti 6 cm. Lascio cadere un ago lungo 3 cm su di essa. Suppongo che l'ago si disponga in una posizione del tutto a caso, diretto in modo del tutto casuale. Con quale probabilità l'ago incrocia una delle rette?  Prova a risolvere il problema con una simulazione (prendi 2 come distanza tra le rette e 1 come lunghezza dell'ago) e verifica che aumentando le prove la probabilità P si avvicina a 1/π, ovvero che 1/P si avvicina a π.  Poi discuti l'attendibilità degli esiti dei seguenti esperimenti fatti praticamente (prima della comparsa dei computer) per trovare il valore di 1/P: Wolf, nel 1850, con 5000 prove, 3.1596 Smith, nel 1855, con 3204 prove, 3.1553 Fox, nel 1894, con 1120 prove, 3.1419 Lazzarini, nel 1901, con 3408 prove, 3.1415929.

Il problema è noto come "ago di Buffon" in quanto proposto nel 18° secolo da Georges-Louis Leclerc, conte di Buffon. Vediamo come possiamo simularlo. Genero a caso, con distribuzione uniforme, l'angolo a lungo cui è diretto l'ago e la distanza h del centro dell'ago dalle rette verticali, o, meglio, genero la distanza dall'asta di sinistra e poi prendo il valore minimo tra essa e la distanza d dall'asta di destra. Ecco che cosa posso ottenere con un programmino in JavaScript, software che è incorporato in tutti i browser. Basta andare qui: http://macosa.dima.unige.it/js/js.htm (puoi vedere anche qui), cliccare "macosa.dima.unige.it/js.com" e mettere nella finestra in alto: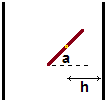

<pre><script> with(Math) {
n=1e3; x=0; for(i=0; i<n; i=i+1)
  { h=random()*2; a=2*PI*random(); d=abs(cos(a))/2; if(2-h<h) h=2-h; s=0; if(h<d) s=1; x=x+s}
document.writeln("n=",n,"  P = ",x/n*100,"%  +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
  { h=random()*2; a=2*PI*random(); d=abs(cos(a))/2; if(2-h<h) h=2-h; s=0; if(h<d) s=1; x=x+s}
document.writeln("n=",n,"  P = ",x/n*100,"%  +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
  { h=random()*2; a=2*PI*random(); d=abs(cos(a))/2; if(2-h<h) h=2-h; s=0; if(h<d) s=1; x=x+s}
document.writeln("n=",n,"  P = ",x/n*100,"%  +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
} </script></pre>

Ecco cosa ottengo arrivando a 100 mila prove:

n=1000  P = 34.2%  +/- 1.4614880045082799%
n=10000  P = 32.44%  +/- 0.8108802606808281%
n=100000  P = 31.678%  +/- 0.4531279756053052%
1/(31.678+0.4531279756053052) < 1/P < 1/(31.678-0.4531279756053052)
0.0311224679 < 1/P < 0.0320257518

È evidente che gli esiti degli esperimenti citati sono tutti poco attemdibili. È particolamente evidente come gli esiti di Fox e di Lazzarini siano del tutto inattendibili. È praticamente impossibile che Lazzarini abbia ottenuto un valore con quasi 8 cifre buone con solo 3000 lanci!
Ecco che cosa si otterrebbe con 10 milioni di prove:

n=10000000  P = 31.83035%  +/- 0.14347521273512284%
0.0312755822 < 1/P < 0.0315588081

Alla fine delle superiori si può calcolare il valore esattamente. Posso ragionare, per simmetria, solo per −π/2 ≤ a ≤ π/2 ed h ≥ 1. L'ago attraversa la retta se h = cos(a)/2. Devo trovare il rapporto tra l'area della figura gialla a lato e quella dell'intero rettangolo. L'area gialla è ∫[-π/2,π/2] cos(a)/2 da = 1. L'area del rettangolo è π. Quindi la probabilità cercata è il rapporto tra 1 e π, ovvero è il reciproco di π.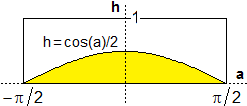

 

Vediamo anche come possiamo simularlo con questo semplice script in cui modifico TruthValue nel modo seguente (poi vedremo come usare R).  Teniamo conto che 1/π = 0.3183098861837907 = 31.83098861837907%.

function TruthValue()
{ with(Math) {

h=random()*2; a=2*PI*random(); d=abs(cos(a))/2; if(2-h < h) {h=2-h}
V=0; if(h < h) {V=1}

}}

n=40960000 31.825283203125% +/- 0.0218342910833447%
n=20480000 31.8223876953125% +/- 0.030877601936424175%
n=10240000 31.809599609375% +/- 0.0436628438885491%
n=5120000 31.79392578125% +/- 0.06174046859282866%
n=2560000 31.8045703125% +/- 0.08732201691047015%
n=1280000 31.82% +/- 0.12350798194797219%
n=640000 31.78453125% +/- 0.17461475799543005%
n=320000 31.815% +/- 0.24700590192161648%
n=160000 31.72625% +/- 0.3490590242946021%
n=80000 31.5575% +/- 0.49293902681561647%
n=40000 31.505% +/- 0.6968123908647875%
n=20000 31.71% +/- 0.987174189616013%
n=10000 32.3% +/- 1.402938282171514%

1/(32.3+1.402938282171514)*100 = 2.967100350799352
      1/(32.3-1.402938282171514)*100 = 3.2365537187083766
1/(31.825283203125+0.0218342910833447)*100 = 3.140001603541853
      1/(31.825283203125-0.0218342910833447)*100 = 3.144313067320735

Ecco lo studio con R.

print(pi,10)
#  3.141592654
#
n=5000; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3198  3.126954
n=5000; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3116  3.209243
#
n=3204; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3093009  3.233098
n=3204; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.31804  3.144259
#
n=1120; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.325  3.076923
n=1120; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.2946429  3.393939
#
n=3408; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3154343  3.170233
n=3408; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3171948  3.152636
#
n=1e4; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.3198  3.126954
n=1e5; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.31815  3.143171
n=1e6; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.318382  3.140881
n=1e7; s=0; for(i in 1:n) {h=runif(1)*2; a=2*pi*runif(1); d=abs(cos(a))/2; h=min(h,2-h); s=s+ifelse(h<d,1,0)}; s/n; n/s
# 0.318449  3.14022

Posso studiare meglio il fenomeno usando un'opportuna libreria; vedi qui, clicca l'indice dei comandi e cerca "simulation", poi clicca anche il collegamento "here" al problema di Buffon:

Pr = function(n) {f = 0; for (i in 1:n) f = f + ifelse(Event(),1,0);
 fr=f/n; S=sqrt(fr*(1-fr)/(n-1)); cat(fr, "+/-", 3*S,'\n'); fr0 <<-fr; n0 <<-n; A<<-fr-3*S; B<<-fr+3*S}
Pr2 = function(n) {f=0; for (i in 1:n) f=f+ifelse(Event(),1,0); n=n+n0; f=f+fr0*n0
 fr=f/n;S=sqrt(fr*(1-fr)/(n-1));cat(fr,"+/-",3*S,'  n =',n,'\n'); fr0<<-fr; n0<<-n; A<<-fr-3*S; B<<-fr+3*S}
Event = function() {h=runif(1,0,2);A=runif(1,0,2*pi);H=abs(cos(a)/2);h=min(h,2-h);ifelse(h<d,1,0)}
more(pi)
#  3.14159265358979
n=5000; Pr(n); 1/c(B,fr0,A)
0.3138 +/- 0.01968936 
#  2.998596 3.186743 3.400081
n=5000; Pr(n); 1/c(B,fr0,A)
0.3256 +/- 0.01988294 
#  2.894499 3.071253 3.270998
n=3204; Pr(n); 1/c(B,fr0,A)
0.3139825 +/- 0.02460159 
#  2.953476 3.184891 3.455653
n=3204; Pr(n); 1/c(B,fr0,A)
0.3205368 +/- 0.02473801 
#  2.896243 3.119766 3.380676
n=1120; Pr(n); 1/c(B,fr0,A)
0.2973214 +/- 0.04099186 
#  2.955840 3.363363 3.901228
n=1120; Pr(n); 1/c(B,fr0,A)
0.3223214 +/- 0.04191434 
#  2.745474 3.102493 3.566244
n=3408; Pr(n); 1/c(B,fr0,A)
0.3157277 +/- 0.02388944 
#  2.944492 3.167286 3.426556
n=3408; Pr(n); 1/c(B,fr0,A)
0.3075117 +/- 0.02371768 
#  3.019056 3.251908 3.523682